Understanding principles | Appreciating concepts | Maths is all about playing with mathematical symbols.
Sunday, 31 August 2008
Inverse Matrix | What is it used for?
If you are good with algebra, you will discover that this inverse matrix way of handling the solution of simultaneous equations is similar, except that they are done as a group, collectively.
The answers to the unknown variables are obtained at one go with this Inverse matrix method.
However, what do you need to know in order to use this Inverse matrix solving?
You have to understand:
1) Convertion of simultaneous equations into a set of matrices
2) Determinant and technique to get its numerical value
3) Minor of the individual elements within the matrix
4) Co-factor of this determinant formed with this set of matrices
5) Transpose of matrix
6) Adjoint matrix obtained with the co-factors and transposed matrix
7) Formula to relate determinant with the adjoint matrix ==> Inverse matrix
8) Matrices multiplication
The list looks amazingly long for matrix novice, but, DO NOT FEAR!
Why?
Matrices consist of numbers only, and simple mathematical operations, nothing abstract.
(The details are not presented here for fear that you will leave this site.)
Slowly research into the above terms and see for yourself that they are "friends" and not "foes".
Happy start to matrices and its application.
.
Monday, 25 August 2008
Graphical Art (Jelly Fish)
Graphical Art (Volcano)
Saturday, 23 August 2008
Differences between Determinants and Matrices
Both contain numbers within. But ......
- determinants are bounded by two straights lines whereas matrices are by square braces
- determinant resulted in a single numerical value, whereas matrices are sets of numbers grouped within the braces
- determinant can be extracted from matrix, but not the other way round
- there are inverse matrix but not inverse determinant
- a scalar multiplier affects only a single row or single column of a determinant, but affects all the numbers within a matrix
The differences are aplenty. But those listed above are the least any maths students or person should know.
Why create such topics to excite maths learners?
Answer: So that maths will be made interesting and challenging (... the informal reply)
With open mindedness, maths is a very fantastic subject to learn and train for. It carries many hard works and beautiful thinking. Thoughts that are simple yet abstract at times.
Any more fun? ..... You are the answer!
.
Wednesday, 20 August 2008
Cramer and Sarrus | How are they related to maths
Who are they?
In which area of maths are they involved?
For those of you who is doing matrices, you will be familiar with their rules, I suppose.
They are famous for creating techniques used in the solution of simultaneous equations.
How so?
Cramer's Rule is a method of solving unknowns in simultaneous equations using division of various determinants.
Rule of Sarrus is a simple way of determining the numerical value of 3rd order determinant.
The two rules, therefore, complement each other to form an easy way to solve simultaneous equations.
However do note that students of these topics use to mix up the 2 rules.
When question states the use of Cramer's and Sarrus rule, they tend to get confuse. THe common notion is that Rule of Sarrus is another method to solve simultaneous equations which is not so.
It is only a technique to evaluate the determinant and get its value. It cannot solve the unknowns in the set of equations.
This is a good problem to get confuse. Why?
Getting confuse means a thinking brain and learning starts to take place. When there is no confusion, there can be two happenings.
- blank or "completely do not understand"
- "completely understood without questions"
Which is which does not matter. What is important is not to disappoint Cramer and Sarrus!
Work hard folks!
Cheers!
:-)
Tuesday, 19 August 2008
A Good Quadratic Solver
Even though you may not use it to solve math problems, you can take this Quadratic solver as a guide to check your answers.
It is a user-friendly tool that can give you the answer easily. Try it!
This is one of the easily available math tools that make maths learning exciting and and interesting. See for yourself.
Quadratic Solver
This solver is provided by Algebra.Com:
.
Log X Is Just A Number
The mistake inter-mixed the principles of algebra with logarithm.
The maths question is to solve the value of x given the expression:
2+ log (5x - 1) = log 3x
The expression, after transferring the "log (5x -1)" to the right side of the "=", became
2 = log 3x - log (-5x + 1) !
Spotted the mistake done ?
Why was the "log (-5x + 1)" in that form?
The correct expression should be 2 = log 3x - log (5x - 1).
What actually went inside the student's mind was confusion between algebra and logarithm. He did not understand the concept of "logging" the (5x -1).
Log X is always a number!
Similarly log (5x - 1) is also a number.
Therefore log (5x - 1) moves as a number, same as in moving algebraic term.
If we have 2 + (x-a) = y, re-arranging the expression, gives us 2 = y - ( x-a).
The term "x-a" is taken as a whole, with change in the sign of (x -a) and not including that of the individual internal "a" and "x". This is basic algebra.
Moving log (5x - 1) is the same. Being a number, it operates equivalent to the algebraic manipulation.
The log (5x -1) is thus taken as a whole and sign change affects only the term as a whole. It does not affect the individual internal "5x" and "-1"!
Part of learning maths is following rules and principles.
The mistake made by the student was a reflection of correct algebraic change, but in the wrong sense. "Log" had converted the term into a number, and that was the mistake not captured.
Being careful with every steps taken in solving maths questions is a discipline one can treasure. This is one of the interesting part of doing maths!
<*_*>
.
"+" Its Many Interpretations
We use them easily in many maths expressions. In normal usage, they are maths operator. But there are some instances where their meaning deviates and is important that the maths learners are aware of.
This deviation to the normal meaning happens to allow maatching to the application.
Let's take a simple example of the "+" operation.
Case 1:
H + H + O = H2O
This is the addition of chemical elements with a different results from normal maaths.
The interpretation differs to suit the chemical equation. It is valid. But not for true maaths!
Case 2:
A + A = A
Why is it not A + A = 2A?
This is an instance of the Boolean Algebra. In boolean operation, there is no "2", being in base 2.
In boolean or digital operation, the "A" can mean a "High" logic or "1".
Therefore, a "High" added to "High" will still give a "High" logic (in the electrical sense).
Thus A + A = A ==> Still a valid add (+) operation in this digital sense.
Case 3:
a++
In this case, the operation is actually an abbreviation of a programming language.
What it really does is to replace the result of a mathematical operation of a + 1 back to itself.
A location called "a" is provided (in hardware) and the results of the operation "a + 1" is placed back to the "a" location. This is again a valid "+" process with a different meaning to the normal maths operation.
The 3 cases highlighted serves to let maths learners know that the symbol "+", though looks simple, is also subjected to many interpretations. Thus everyone needs to be aware of its matching to the specific applications.
:)
Mental Alertness In Maths Calculation
Did you make simple maths error especially after a certain period of performing maths calculations?
Our mind has to have the strength and stamina to stay active and alert to have 0% error.
This is not a maths problem. Rather it is a psychological problem.
How then are we to minimise, if not eliminate, these simple maths errors that we hate to make?
Below I list a simple trick that I often used and advise maths learners.
- Before starting to do any maths assignment, or test, or examination, scan through the whole paper to scout out the simple and difficult questions.
- Start off with the complex questions or those that you are not that confident with. You need the attention to "attack" those questions while your brain is still alert. (Note the time factor too, otherwise, you may consume too much time for them leaving little time for the simple ones!)
- After completing the complex questions, you will be more relax mentally to solve the other questions. And given the simplicity, less error will be made since you have scanned through the paper initially and has better confidence in dealing with them.
This is a proposal that balance mental alertness with solving math questions.
Maths solving can be taxing, but with proper strategy, you can lessen the anxiety and, in fact, after more practice, like and enjoy maths.
:-)
Math Challenge 9
Add five to it.
Multiply the total by two.
Subtract the original number twice.
Is the answer "TEN"?
Thinker: How is it done?
.
Math Challenge 8
(Do not tell anyone).
Multiply the number by three.
Add six to it.
Divide the total by three.
Subtract the result by the original number that you kept secret.
Is the final answer "TWO"?
Thinker: How is it done? ==> Use Algebra
.
How To Draw Best Fitting Straight Line
The data given are mostly random values that may not be lying on a straight line.
Therefore the technique of drawing this straight line on the graph becomes a crucial skill as it may results in producing inaccurate answers or outcomes.
An example is presented here for discussion.
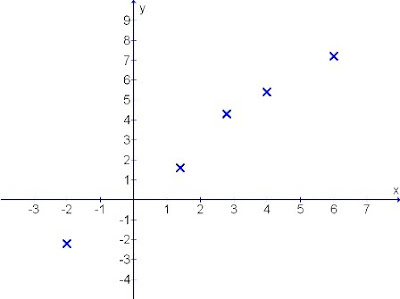
Diagram 1: Various random co-ordinates scattered over the sheet
How do we plot a suitable straight line from these few scattered co-ordinates?
Many "funny" ways exist that reflects poor understanding of the purpose for straight line plotting.
Way one:
Connecting up the points in sequence ==> Results in non-straight line end-to-end.
Way two:
Connecting the extreme two co-ordinates ==> Results in unbalanced straight line (diagram 2)
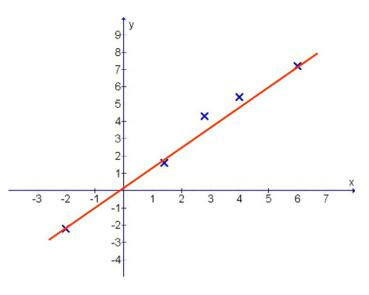
Diagram 2: Uneven gaps between points and line drawn
Here you can clearly see that there are 2 points that are above the straight line by a certain gap. The spread of the random points are not evenly balanced about the straight line drawn.
Let's see a better way to fit the line to these randomly scattered points. (Diagram 3)
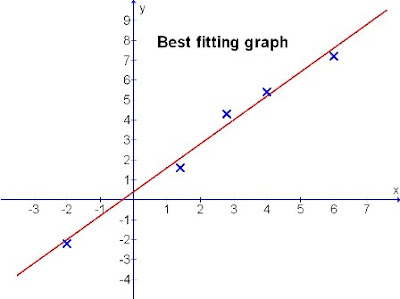
Diagram 3
In diagram 3, you can see that the scattered points are evenly balanced across the length of the straight line drawn. The gaps of the crosses are almost the same through.
This is termed the "Best fitting straight line".
Therefore in plotting a straight line, it is the evenness that counts. The spread of the points has to be balanced so that the individual errors of the given data to the line can be minimised. The line drawn is then one that will produce a more accurate results.
Never imagine that so much thoughts are needed just to plot a straight line graph, right?
:-)
How To Get Gradient and Intercept from Two Points
In maths, to obtain the equation of a line from two given co-ordinates, we inevitably think of graph plotting. This is one good way to obtain the answer by finding the gradient and intercept.
Let's take an example.
2 points: (1, 5) and (3, 11) are given. What is the straight line expression?
By plotting these two points on a graph, we can easily determine the gradient and intercept, and then the mathematical expression for the equation.
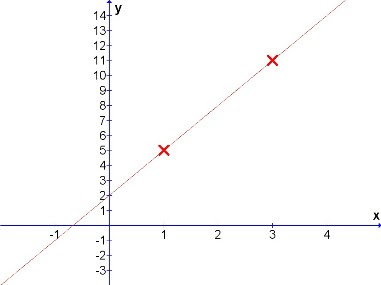
Diag: Graph with 2 points.
From the graph, to determine the gradient, we can check:
- increase of the vertical unit with reference from the 2 points as 11 - 5 = 6 units, and
- increase of the horizontal unit from the 2 points as 3 - 1 = 2 units,
Gradient = change in vertical / change in horizontal = 6 / 2 = 3
The next item is the intercept, and directly from the graph, it showed the value to be 2.
Therefore, the straight line expression comes to y = 3 x + 2.
This graphical method is OK, simple and easy to do.
But is this the only way to get the straight line expression from 2 points given?
No, there is at least one other method. Don't forget maths is exciting and amazing, if one wishes it to be.
What is the other way? The answer is the use of simultaneous equations!
How so?
Note, given 2 co-ordinates and having to find 2 unknowns satisfies the basic requirement to set up 2 equations for simultaneous solving.
We know the general straight line equation to be y = mx + c.
Therefore with the known co-ordinates,
11 = m(3) + c -----(A)
5 = m(1) + c -----(B)
By elimination method, (A) - (B), gives,
6 = m(2) ===> this gives m = 6 / 2 = 3 (The gradient!)
With m = 3 found, let's put back into equation (B),
5 = (3)(1) + c ===> c = 5 - 3 = 2 (The intercept!)
Thus, the straight line equation is y = 3 x + 2. This is the same as the one obtained with graphical method.
Therefore, from the simultaneous way, we can still obtain the expression from the 2 given co-ordinates, without plotting the graph.
Either which way is fine.
What is interesting is that once you master the principles of maths, you can be flexible to choose the method that you like and still arrive at an appropriate answer.
Enjoy maths! :)
.
Monday, 18 August 2008
How To Reduce Stress In Learning Maths
"How to remember?"
"Why teach so fast?"
"Any simpler method?"
These are sampled questions that express the stress and anxiety that many students faced.
Though some of the components of teaching and learning can be simplified, they take time to implement with due consideration for many other factors like curriculum, key learning objectives, and quality.
What then can we do to lessen the stress that keep on coming?
The answer is to stay focus and be aware of the key objectives of the topic.
If the maths topic is about logarithm and its various laws, the objectives should be to apply the logarithmic laws to solve any related maths questions.
Do not ask questions like :-
"Why must I write the base with a smaller font size?" and
"Why do I need to add the individual logs to form a logarithmic product?".
Asking questions is definitely good for learning, but in these instances, the focus is not to dig out the history part of logarithmic studies.
The main aim is understanding the application of the laws in order to apply and solve problems. It is simply just that!
Trying to find out more than what the maths syllabus calls for within the short time frame is tantamount to facing learning disaster.
Just know that analysing too much into a subject or topic is equivalent to paralysing the learning mind. Stress, thus, appears and starts getting on your nerves!
Remove the unnecessary questions that blocks the main objectives and move along with the requirements. Pick up the extras only if you have the time and in a comfortable and relaxed mood.
Why cause undue stress and anxiety upon yourself if the key matters in maths learning is not treated properly?
Contain the scope and stay focus!
Do not dwell on things that are not the main issue and causing mental blockage. Accept what is taught for the moment, and coming back for in-depth understanding after mastering the necesary.
(NOTE: You still have to fully understand the topic, the approach explained here is to "buy" time to release some stress.)
This way, learning maths will not be that stressful and will become fun, since the basics can be managed comfortably with understanding.
:-)
Ways To Improve Logical Learning Part Of Maths
Each of us has one particular dominant style. Knowing which one will thus serve us good. However, the learning style itself is still not enough, we need to also know the types of intelligence we possess.
The learning styles are used to gather information and ideas, through the senses, for the brain. But how do we process the information captured afterwards depends much on the intelligences that we also have.
In maths learning, what we need is the logical / mathematical intelligence.
This lets us do all sort of computations and comparisons that maths requires.
An example is the conversion of an expression in logarithmic form to its index form (and vice versa).
logaY = X <==> aX = Y
Though, this conversion seems simple enough, it is found that many students still have difficulties in converting the above. Do they lack this logical intelligence?
The answer is "maybe" and "maybe not".
They may have possess this logical intelligence, but has not yet enhanced it.
One way to offset this weakness in the logical comparison part of intelligence is to introduce the visual intelligence into maths learning.
What is this visual intelligence?
This is the "appearance" aspect of information processing. Here, colour, shapes, and the likes are linked up to the information.
Why introduce the visual intelligence?
The main reason is to bridge up the right and left brain, a theory that is now well-known and practiced throughout the learning and teaching communities.
Now, let's see how we can solve the logarithmic and index conversion through the use of the visual intelligence.

The examples above showed two very interesting ways to enhance the learning. :)
The first one is to replace and "beautify" the symbols with pictures or graphics to arouse retention ability.
The second one is to make use of colours to strengthen the symbols and their placements.
By seeing pictures and colours, although they are no way close to any maths topics, the learning of maths is greatly improved especially for the logical comparison portion.
Therefore, if possible, introduce as many "visuals" into maths as you can. They will make maths learning a totally new experience. Take care of intelligences and intelligences will take care of you.
Inspired ?
:=)
Benefits Of Knowing How To Solve Quadratic Equations
The generic quadratic equation is y = a x2 + bx + c.
We know there are various methods to handle the quadratic equations.
There are:
- Factoring
- Completing the Square
- Quadratic Formula
- Graphical
Mastering all these techniques allow anyone studying maths to have the flexibility of choosing a better or suitable method that fits the nature of the question.
However, do note that if there is problem learning all these techniques at one go, click here to get some pointers.
What is the benefit?
Many maths questions are actually quadratic in expression. They may not appear so, but, on closer look, they are.
Examples:
- 3 cos2 A + 2cosA + 4 = 0
- 2 (log Y)2 + 2(logY) + 3 = 0
- 4x + 3(2x) - 5 = 0
- 5x-2 - 7x-1 - 6 = 0
Being able to handle the generic quadratic equation solving means having the potential to solve numerous other types of quadratic equations as listed above.
What is the obstacle if you still cannot map the quadratic solving method to the other types of expressions?
Tips:
- Stare at the given expression
- Identify the terms that matches the x2 format.
- Identify the other two terms through the "x" format and pure number format.
- After re-writing the questions in the generic quadratic form, apply any of the method to solve this quadratic equation.
And that's all.
Simple isn't it?
Thus, mastering any one method of handling quadratic equation allows anyone to solve many other types of quadratic equations. Therefore, it is worth the time and effort to know solving these type of mathematical expression.
Bonus information:
Let's look into this example
The first term can be modified to 5(x-1)2.
The second term can be modified to 3(x-1).
The last term will be obviously the pure number "2".
Selecting the use of quadratic formula, we can say that a = 5, b= -3 and c = -2.
Next, just apply the quadratic formula and you are close to the two answers (roots) of the equation,
x-1 = -4/10 or 1. Clear?
If not, read again... Our brain needs some mental exercise at times.
.
Indices & Logarithm - Less Mistakes with Proper Writing
Many mistakes and confusions were made due to improper writing of the above two items that are very much key to mathematics.
Two of the topics that are commonly populated with writing errors are Indices and Logarithm.
Indices: ax = Y
Logarithm: lognA = K
From the above two examples, it is apparent that writing is crucial to give correct meaning to mathematics.
Writing therefore is an important skill while doing these two maths topics.
Discipline is needed here to maintain consistency.
What do I mean?
Let me give an example.
log2 xy = log2x + log2y
The above is a correct expression written with proper size and positioning.
If writing discipline is not maintained, it may end up as:
log2 xy = log2x + log2y (size and position error)
Do you notice the change in meaning when size changes?
The subscript "2" representing "base 2" is conveyed as "2 times y"!
This is the result of a simple "slip" of the hand in writing the size of the "2".
Can this mistake be allowed?
I guess NO!
Why run the risk of marks being deducted or effort wasted in getting wrong answers?
Write properly is the only answer to less mistakes, if not at all.
If ax = Y is written as ax = Y, how do we expect to get correct answers?
Here, you realise that maths learning is not just about mathematical concepts, human discipline and strength of concentration matters also.
Being able to write clearly and presentable is a noble capability that we should be proud to demonstrate to anyone. Strive to be focused and discipline when dealing with maths.
Happy writing! :P
.
Know Your Limits While Learning Maths
Is it good then to master all the techniques taught?
The answer is to know your limits.
If you are stressed up learning so many methods, let go of the ones that you find uncomfortable with. Master the one that seems to be the best and easiest to you.
Stay on with this chosen technique of solving problems, and apply it to similar maths questions. This is the first step in the principles of correct mathematics learning.
However, do not be complacent and stay stuck! Having more methods to solve a certain maths problems is always a better and sensible course of action any maths learners should aim for.
After mastering the first selected method, move on and try using another technique that was taught. Practice till it becomes comfortable and an easy tool to use.
In mathematics, flexibility is the norm. Questions are always varied, and thus, solution has to follow suit. It is this nature of solving mathematics that makes a good maths learners achieve much in his later life.
Knowing one's limit is thus important especially when dealing with mathematics. Focus on one method first as too many at a go will only mess up the curious and greedy mind.
Understand that maths problem can be solved through the use of any one method. Even if the steps are more, it is still a way to obtain the answer. Slowly after mastering the selected method, you can explore another method that can shorten the solving process.
At least you are now more relax as you can fall back to the first method if the new technique cannot be comprehended finally.
However, having said that, do review the maths syllabus. Some syllabus do spell out that the students have to master a few methods to solve a certain type of maths questions. For that matter, you are left with no choice but to deal with them accordingly. Seek for help if necessary, and do not simply give up!
Finally a message that I like to share. "Although practice makes perfect, good practice is the one that makes perfect ultimately!"
Choose the correct principles of learning and you will not go wrong. Know your mental limits.
;)
Solving Maths Develops Plan Foward Capability
One of this skill is the ability to see the "path" to the result. This ability, however, is obtained when we are able to plan what to do and reveal the intermediate goals.
Solving maths is like a mini-warfare where the enemy is the result that has to be obtained. Every steps that we take to achieve our goals has to be planned for.
We need to think ahead in each steps of computation and be capable of using whatever tools available to clear the obstacles lying in front of us.
Solving maths, thus, is a good platform for anyone to gear themselves for a future of planning, or to have better planning capability.
The steps required to solve a maths problem develops one to be able to plan forward. The steps taken at every maths operation serves a certain purpose to simplify mathematical expressions or eliminate unknowns.
Studying and doing maths is therefore a necessary part of human development in that it allows the learners to develop their mind to solve real-life problems through proper planning.
So to developing minds, cheers to maths!
.
Why Do We Study Quadratic Equation?
But after all these, what is the purpose?
This is the question many students of maths studies ask.
Do we need this "quadratic" knowledge in working life?
See the diagrams and photos below. They will enlighten you.

The communication dish is parabolic in shape. Parabolic is the equivalent to quadratic mathematically. Engineers need to understand quadratic equation to design this beautiful profile.
 This wok is designed using quadratic expression. With this, food can be fried to our liking!
This wok is designed using quadratic expression. With this, food can be fried to our liking!Without quadratic equation, who knows how a wok would look like.
.
.
Here you see that eye-glass lens are constructed with curves matching that of the quadratic equation.
Light is thus controlled to give good image to our eyes.
Quadratic equations to the rescue, right?
.
.
.
.
.
.
Other examples are:
1) Distance travelled given by the quadratic equation s = ut + (1/2) a t2
2) Electrical characteristics of a MOSFET (Transistor device)
i = k [(Vg - Vt)VD - (1/2)Vd2]
So now do you still wonder why you study quadratic equations?
Maths do have a purpose in our daily life. Rest assure that you are studying maths for a good cause.
:-)
Merit of Grouping in Maths Solving
Example is the solution of Partial fraction, that is highly needed in calculus.
One of the steps needed is the comparing of coefficients to extract out equations to determine the numerators in the individual terms of the partial fractions.
An example is shown below.
x - 3 = A x2 + B x (x + 1) + C (x - 2)
How do we solve for the unknown A, B and C?
One useful technique is to do "grouping" of relevant terms.
This is a simple yet powerful method that make the process of solving maths less confusing as it serves to gather common or liked term in the same boundaries.
What I mean is ....
From the above example, we can rewrite them as,
x - 3 = A x2 + Bx (x + 1) + C (x - 2)
==> x - 3 = A x2 + Bx2 + Bx + Cx - 2C
==> x - 3 = (A + B)x2 +(B + C)x - 2C
Here, you can see that the coefficient of the terms can be equated nicely to be :-
x2 term: (A + B) = 0
x term: (B + C) = 1
Constant: 2C = 3
From herer A, B and C can be easily determined comfortably.
Thus, grouping has the ability to simplify the thinking steps due to clarity as reflected above.
Another example is in Indices simplification.
Take the example of 10n5n/2 / 20n/4.
We cannot see any way to combine the different base number (10, 5 and 20) unless we split them into their lowest factors. (Don't lost focus now, we are aiming for Grouping technique!)
10n = (5 x 2 )n
20n = (2 x 2 x 5)n
Rewriting to prepare for grouping,
(5 x 2 )n5n/2 / (2 x 2 x 5)n/4
==> 5(n + n/2 - n/4) 2n- n/4 - n/4
==> 55/4n 2n/2
Here again, you can see the merit of grouping the common base number in order to perform the Indices operation.
Maths is "tricky" at times, but isn't this to train our mind to stay active and flexible to counter any challenges put forward. It actually enhances our self-esteem and confidence to handle problems in real life.
Happy grouping .....
:-)
Indices | Big and Small concept
a2 means a times a, or simply a x a.
(a + b)2 means (a + b) x (a + b).
(anything)3 means (anything) x (anything) x (anything).
Therefore, from above examples, we can see that "anything" operated by a small number higher up above it means repetition by that number of times (defined by that little number).
Mistakes normally made:
(a + b)2 ==> a2 + b2 This is wrong!
a2 - b2 ==> (a - b) 2 This is also incorrect!
Reason
The "2" is a power and not a factor. It means repetition. And therefore cannot be factorised.
The "2" is written above the normal line (called the base), and thus has "bigger" power than the base element.
The correct answer to the mistakes:
(a + b)2 = ( a + b) ( a + b) = a2 + 2ab + b2
a2 - b2 = ( a x a ) - ( b x b ) = (a - b ) ( a + b ).
To summarise, the "smaller" number (or letter) makes the "larger" base repeats the number of times indicated by that small number.
Principles of mathematics and its indices' concept .....
Understand the principles and concepts, and you will be fine.
For more common mistakes in indices, click here.
.
Tips To Reduce Errors Doing Simultaneous Equations
Though the mathematical operations are simple, mistakes made while solving simultaneous equations are aplenty. The errors are mostly "slip-of-the-mind" human errors.
To review the elimination method employed to solve simultaneous equations, please click here.
How then are we to reduce these careless errors?
Here, I propose 2 tips.
Tip one
Make use of addition instead of subtraction to eliminate the selected unknown.
Example: ( to eliminate unknown "y")
7x + 2y = 11 --- (A)
-5x + 2y = -1 --- (B)
In normal doing, we perform (A) - (B) equation subtraction. But what is the risk?
The result may end up as 2x + 0 = 10 !
The correct answer should be 12x + 0 = 12.
Why the error?
This is because our brain is use to addition more than subtraction. Therefore the "slip-of- the-mind" error happened.
Mentally doing 7x - (-5x) is harder to operate with.
Refer to this post to understand why our brain likes addition.
So how?
Negate the equation (B) so that we can perform addition.
(-5x + 2y) times (-1) = -1 times (-1)
will become 5x - 2y = 1 ----(C)
Rewriting the question,
7x + 2y = 11 ----(A)
5x - 2y = 1 ----(C)
This becomes simpler!
We now need to ADD the 2 equations. (Instead of the risky subtraction).
(A) + (C) : 12x + 0 = 12 <== This is the correct result that we want, risk-free!
Message: Negate the unknown variable of one equation and do ADDITION to remove it.
Tip two
Avoid making the number (coefficient) bigger through multiplication.
Example:
9x + 2y = 13 --- ( K )
x - 4y = -7 --- ( L )
Here, we have the option to remove either the "x" or the "y".
Which to select depends on the proper selection of multiplication factor in order not to make the coefficient big.
Case 1: Remove "x".
We need to multiply equation (L) by 9 to cause the first term (x) to be the same as that in equation (k), so as to eliminate the "x" unknown.
What happened?
Equation (L) became 9x - 36 y = - 63 !
Look at the coefficient of "y" ===> It became a GIANT!
Case 2: Remove unknown "y".
Multiply equation (k) by 2. This produces equation (k) as 18x + 4 y = 26.
This is still manageable. And less error will occur since big number is harder to handle.
Message: Seek to multiply coefficient such that the resultant equation has smaller number.
I have seen many maths students fumbling with these simple operations, and making many unnecessary mistakes.
I do hope that these two little tips will aid you and any maths learners of simultaneous equations to reduce errors.
:-P
Our Brain Is Tuned For Addition Versus Subtraction
Do you make more mistakes doing subtraction than doing addition?
If the answers to the above questions are all YES, you are not alone.
We are "programmed" since young to add more than subtract.
Do you count things starting from 1 up or down from 100?
Does the page number of books starts from 1 up or down from the last number?
Does the date on a calendar month starts from 1 up ?
Day in day out, we are bombarded by addition of numbers through counting up. It is not accidental though. It is due to the fact that we do not know the maximum in those counts.
Therefore, we are accustomed to addition and will do better with this maths operation than with subtraction.
Try doing this:
- y = 44 + 36
- y = 44 - 36
- y = 60 + 53
- y = 60 - ( - 53)
We can do the above simple maths questions easily.
But, honestly, did you take a longer time to compute the subtraction?
There is a slight mental block compared to addition, right? Mine does.
There is nothing wrong with this. What I like to bring to your attention is the fact that knowing addition is the brain's preference, we can minimise maths error by aiming for addition than subtraction, if possible.
If we are to do a maths operation y = 55 - (3 + 6), do the (3 + 6) first, followed by the subtraction.
Avoid doing y = 55 - 3 - 6, with 2 subtractions involved. Although mathematically it is correct, why take the risk?
It's the same for calculating y = 53x + 16x than doing y = 53x - (- 16x).
Did you get the message? Understand how your brain works and tweet the mathematical process for a less risky computation.
;)
Principles of Learning (Mathematics)
Before we start learning anything useful, we need to question ourselves over its purpose.
If the answer to it is sufficient enough for you to strike on, you are in the correct path to a better future.
However, what is the mental approach to learning, before actual content acquisition?
Is the ownership of learning clear?
These are the questions you have to answer before you set out on the bright journey of learning.
The key issue here is OWNERSHIP of learning.
Besides learning the essential principles of mathematics, the crucial principles of learning has to be handled well too. Do note that both go hand-in-hand.
Principle of learning takes into account the idea that learning is the sole ownership of the learner.
The teacher is, just after all, a catalyst to speed up the learning process. He is there to address any questions that may be harder to solve or missing links that may unknowing been left out during the course of lesson delivery.
But to have a fruitful learning outcome, you must know the fact that you are the ultimate target of the process. You have to constantly remind yourself that "I am the one learning".
Whether can the teacher teach well or explain properly, the learning still goes back to you. (Do not blame anyone for failure to learn!). It becomes an excuse to deviate from the proper.
So, the principles of learning has to be clearly understood before principles of mathematics can be effectively captured.
Mathematics learning will then be a wonderful learning journey.
Wonderful here does not mean easy-going though.
Without decent struggle in learning and thinking, retention of knowledge will not last long. This is a well-known fact! (Struggle here means the mental processing of knowledge, past and current).
Study hard (and smart), and know that you are the final gem that any teacher would like to polish, provided you start off with the correct mindset.
Cheers to learning and cheers to you, the mathematics gem.
Maths Is Interesting!
.
Analysis of Maths Error
This is possible, provided the learners pick up the error made and understand them through detailed analysis.
I came across an error that puzzled me for quite some time.
The error made: Inverting y = 2x + (1/x) became 1/y = (1/2x) - x
What actually happen in the thinking during the math manipulation?
Understanding the thinking will definitely help in resolving the issue and prevent further mistakes made.
Here, I believe the student:
- confused "flipping" cards with the basic concept of maths (flipping the left y does not equate to individually flipping the right mathematical terms)
- confused the property of indices ( 1/a = a-1) with this operation, resulting in the last term having a shocking "-" appearing after the inversion of denominator to numerator placement.
- lack practices to enhance the algebraic manipulation during the learning phase. Knowledge is not retained.
Analysing maths error is not an easy task if done alone, and without guidance.
The thinking part is an abstract art of the mind. If there is no communication to reveal the mental procedure in solving the math question, a skilled guess has to be made especially by those teaching maths.
If guidance is not available, textbook will be the next best alternative to answer for the mistake encountered. Go back to basic to dig out more understanding.
The approach is to question and question till satisfied. It will cover most aspect of the learning objectives.
However, do note that identifying and analysing maths error is a great learning process.
It serves to filter out current bad learning habits and replaces the gap with proper systematic steps. This is of much importance especially in maths where every steps count.
Therefore, do enjoy "debugging" your maths error. It is fun and not meaningless!
Errors do tell many stories. Just be friendly to them.
:-)
Linear | Angular Speed
- Linear
- Angular
Linear speed is defined as the distance travelled for a given time.
Angular speed is defined as the angle covered for a given time.
Are they proportional ?
Or are they related in any sense?
Let us take 2 pendulums hung on a slim rotating rod for analysis.
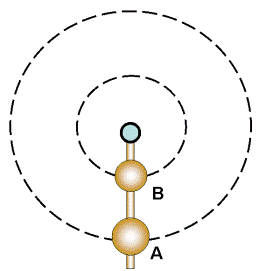
If the 2 pendulums (A and B) rotate one full cycle, the time taken by them is the same.
They covered the same amount of angular distance (360 degree) within the same amount of time.
This showed that they have exactly the SAME angular speed.
But is the Linear speed similar?
The length of the 2 circumferences travelled by the individual pendulums are not the same.
The linear length or distance is therefore NOT the same.
Length = 2 x (pi) x radius.
They took the same time to complete one full cycle, though.
The linear speed is thus DIFFERENT, having travelled different length for the same amount of time.
In this case, the angular speed is the SAME whereas the linear speed is different. Pendulum A has a higher linear speed compared with pendulum B.
Can the angular speed be different and linear speed made to be the same?
If the same slim rod is used, the answer is NO.
But if they are held by different rods, like that of the traditional analogue clock, the answer is YES.
For the linear speeds to be the same, pendulum A has to take a longer time to complete one cycle compared to pendulum B timing.
In this case, their linear speeds are the SAME while the angular speed will be DIFFERENT. This is so, since, same angular coverage but different time taken.
Why are we talking so much about this?
This is an "old" principle that was applied to the famous grandfather's clock. The setting of the pendulum position along the swinging rod (or string) is the key to the time accuracy of the clock. Ancient people has used this understanding to produce something useful for their daily needs, and this is mathematics!
Wonderful isn't it? :)
.
How To Estimate Numerical Answer
It called for logically thinking and is done on a case-by-case basis.
Take for example, 302 x 11.
What is the estimated product of the 2 numbers?
We can choose for it to be 300 x 10, which gives 3000.
But how about being more accurate in our estimation?
300 x 11 gives 3300 !
We can use "11" instead of closing in to "10" of the first instance.
Logical thinking at play here...
But why choose "11" instead of the "10"?
The answer is simple.
Since the first number is 300, multiplying it with "11" is still within any person's ability. Therefore using "11" as part of the estimation is closer to the actual answer.
Now, how about 314 x 11?
Here, the answer estimated will be 310 x 10 = 3100, to be practical.
310 x 11 will be harder to estimate. Therefore "10" is chosen in preference to "11" as in the case of the previous example. (We are not talking about mental maths, but maths for "normal" people.)
Estimation, thus, calls for a fast but accurate production of numerical answer. It involves thinking and choosing numbers that are easy to handle.
Estimating answers can be fun as shown. It can be a challenging game where students aim to be first to give the most accurate answer.
Have fun estimating! :-) It gets more interesting as you go on.....
.
Volume and Surface Area | Geometrical Relationship ?
However, have you wondered what is the relationship between them?
If we want to maintain the volume of an box but reduce its surface area, is it possible?
Or does the volume ALWAYS increases with increase in its surface area?
How about reduction in surface area? Will the volume also reduce?
Let us throw some numbers into an example to figure out the answers.
For simplicity, let us use a simple box. (Diagram 1)

<== Diagram 1 Box of diagram 1 has a : Volume = (2 x 8 ) x 4 = 64 cubic units
Surface area = 2 (2 x 8 ) + 2(4 x 2) + 2(8 x 4) = 112 square units
.
.
Let modify the box (Diagram 2) to another dimension and see its geometric parameters.

<== Diagram 2 Volume = ( 4 x 4 ) x 4 = 64 cubic units
Surface area = (4 x 4) x 6 sides = 96 square units
Note, the volume remained but....
the surface area has reduced!
This saves material, right?
How about another dimension (Diagram 3)?
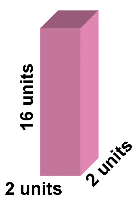
<== Diagram 3 ( A tall box!) Volume = (2 x 2 ) x 16 = 64 cubic units
Surface area = 2(2x2) + 4(2x 16) = 136 square units
What now?
The volume again remained,
but the surface area has increased!
.
What is the conclusion from here?
It is observed that althought the volume of the box has not changed, their surface areas has changed. The direction of change( increase or decrease), however, is on a case by case basis.
This concluded that there is no relationship between volume and surface area of any object.
Therefore don't be tricked into reckoning that surface area increase will cause a definite increase in volume. Likewise for reduction also.
Hope you gain much from here.
Geometry is exciting and mysterious at the same time, right?
For relationship comparsion between another set of geometrical parameters, perimeter and area, click here.
.
Simple Flipping of Math Terms
Many weird answers can come out when done wrongly.
Look at an example of changing numerator to denominator of terms in an equation.
Example: Express y in terms of x for the equation (1 / y) = 5 + x
If the answer is simply to "flip" numerator to denominator,
getting y = (1/5) + (1/x), did the student learn his lesson?
Yes, he applied the concept of x / y = a / c ==> y / x = c / a neatly, but......
something went amiss!
First loophole: Student did not understand the meaning of "="
Second loophole: Student did not understand the meaning of summation
Why?
* Right Concept
First item:
The "=" symbol means whatever collectively on the left equals whatever collectively is on the right side.
Second item:
The "+" symbol means terms are added up to form a bigger piece of "something".
This bigger piece of "something" therefore operates as a whole, and not as individual terms.
The correct answer, hereby, should be, following the above 2 concepts,
(1 / y) = 5 + x ===> y = 1 / (5 + x)
The whole of "5 + x" acts as a collectively bigger piece of "something", and is flipped together as a single piece.
Note, however, here the word "flipped" has many "stories" within it.
Like to hear the "stories"? Read on....
Flipping is an abbreviation for the cross multiplication operation.
Mathematically speaking, it is
1/y = 5 + x ==> Multiply both side by "y"==> (1/y) * y = (5 + x) * y
==> 1 = (5 + x) * y, the "y" is brought over.
Divide both side by "(5 + x)" ==> 1 / (5 + x) = [(5 + x) * y] / (5 + x)
==> 1 / (5 + x) = y .The correct answer.
Finally, at long last, we obtain the outcome of the "flipping".
You can see from the above that if you understand the math principle, you can actually do simple flipping of numerator to denominator, which those ignorant will not be able to comprehend.
They will simply follow the flipping and will get flopped at the end.
Message:
Understand what you are doing. Equations in algebra can reveal your ignorance!
.
Math Challenge 7
2 0 2 0 ?
This is not that difficult if you have attempt the challenge in this link.
.
Math Challenge 6
It is not advanced math that we are talking about.
Just elementary level is good enough to solve this thinker.
Enjoy!
.
Maths Challenge 5
Find the numerical value for the power (x) of both bases such that,
1233 = 12 x + 33 x
Sunday, 17 August 2008
How To Study Math Wisely
But, whichever method one selects and sticks with, an important learning concept is reflected in the Pareto Ratio.
What is this all-important "Pareto Ratio" about?
Pareto ratio is simply a 80 /20 ratio. Though it is simple, its impact to many things are fantastic, and is the deciding element that constitutes wise and effective learning.
What do I mean?
Pareto ratio actually allows us to understand that 80% of the work are done by only 20% of the people.
And 80% of knowledge can be mastered from 20% of the learning material!
This is good news, isn't it?
Yes, it is true. But where is this 20% of the key learning material?
In math textbooks, this important 20% normally lies at the beginning of a new topic or chapter. It consists of the principles and concepts portion within the complete chapter.
Here, knowledge is "told". After this portion, worked examples follow up to demonstrate the application of the concepts and principles of the new topic. At the end of this worked examples and explanation, comes the exercise part for student to practice.
Take a look at any math book on hand. The flow is almost the same with slight deviation to make it outstanding.
The worked examples and exercises constitute the 80% of the learning material that only serves to enhance knowledge. They are important though and should not be ignored!
The message here is that to really master math, focus should be placed at the front 20% of the notes. Understand deeply the concepts and principles within it, and then move on to apply the learned knowledge to test for comprehension of the materials. This is learning math wisely.
Some math learner do otherwise by jumping directly (and impatiently) into the exercise even before a decent level of understanding sets in. This is academic disaster! Avoid it to save time and frustration.
Thus, to learn wise, aim for the 20% and you are effective for the other 80%.
Wonderful right? :)
.
Mathematics Graphics Helps In Better Understanding
Though the questions and explanations may come in the normal English or any equivalent first language, mathematics still consists of symbols, abbreviations, variables and mathematical operators, besides the numerous expressions or equations.
Learning and teaching mathematics, thus, become a chore for those "newbies" as well as those who detest the subject.
Graphics to represent mathematics meaning is therefore a welcome move for them. Although not all mathematical expression can be presented in graphics, it is a better option in term of knowledge retention.
Take an example of solving the simultaneous equations.
Example 1:
Solve y = 2x - 4 and y = -x + 6
To the mathematics learners, this may seem daunting even after explanation. They may not be able to visualise mentally what really is these 2 equations doing, not to say, solving them.
However, if the question is shown in graphics or converted likewise, the understanding will immediately be clear.
Compare the above "worded" question with the "graphical" question shown below.
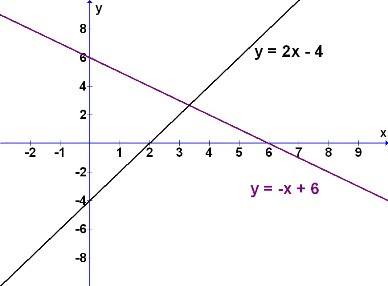
From the graphical interpretation of the mathematical question, it is easier then for the students to understand what is needed. The equations are here clearly shown as lines that intersect at a common point. See the advantage now?
Let's see another example.
Example 2:
The all-famous Pythagorean Theorem is presented as x2 + y2 = z2.
But this is a simple mathematical expression or formula, and that's all (to them).
What actually does it means? Besides pure memorising, what else?
If this Theorem is presented in the graphical form (below) , you will see the difference.
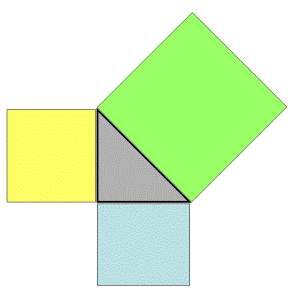
Here the idea that the "squaring" of the sides are related through the Theorem will be easily accepted. The message of the Pythagorean Theorem as areas of various squares will be captured and locked mentally for understanding and retention with ease.
Why is graphical form a better technique of learning and teaching?
This has to do with our brain. It is well known that our right hemisphere of the brain is for image, and the left hemisphere is for logical matters including studying for mathematics.
This graphical learning and teaching, therefore, goes in line with well-known and accepted method of linking right and left brain for better comprehension.
For mathematics learners, it is hence a merit to be able to convert most mathematical knowledge to images, if possible (although it is understandable that not all is possible).
For mathematics teachers, use graphics if possible to save your breath.
Happy imaging !
.
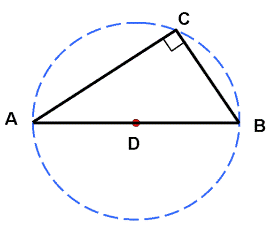
Who Says The Compass Triangle Is Right-Angled?
Look at this post for details on what I am talking (or rather writing) about.
However, the question is how do we know it is truly a right-angled triangle?
The answer is "Go back to basic and prove it is!".... (or it is not)
This ability to prove will enhance your understanding of its principles.
Let the spirit of the mathematician starts flourishing ...
A diagram to simplify explanation is shown herein.
Our target: To prove that Angle C is 90 degree.
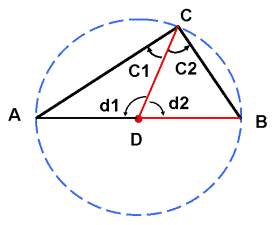
Two key items exist here. They are:
1) Length DA = DC & Length DC = DB,
since they are the radius of the circle
2) Angle C1 = Angle A & Angle C2 = Angle B,
due to the facts in item 1) above.
These 2 key points will ensure that angle C is 90 degree (or right-angle).
Moving on ...
Angle d2 = 1800 - Angle C2 - Angle B = 1800 - 2 x (Angle C2)
Angle d1 = 1800 - Angle d2
Which makes Angle d1 = 1800 - [ 1800 - 2 x (Angle C2) ]
This produces an important observation: Angle d1 = 2 x (Angle C2).
Also Angle A + Angle C1 + Angle d1= 1800, which also means,
===> [ 2 x Angle C1 ] + Angle d1= 1800.
Re-writing the above gives [ 2 x Angle C1 ] + 2 x (Angle C2) = 1800
Factorising the above equation yields:
2 x (Angle C1 + Angle C2) = 1800 ---(1)
Hang on, we are coming to the end ...
(Our target) Angle C = Angle C1 + Angle C2
From equation (1),
we can show that Angle C = Angle C1 + Angle C2 = 900!
Therefore, it is true that
Compass Triangle has Angle C as right-angle.
Hurray!! Eureka!!
Fall back to maths basic if in doubt. The skill picked up will serve you good in the application of maths theory.
:P
How To Draw Right-Angled Triangle Using Geometric Compass
One way is to make use of a protractor.
Another way is to use a try square.
But what if you have only a geometric compass, how do you do it?
(Not the compass that give you directional bearings of north, south, east and west!
It is the one that let us draw circle with.)
Don't worry. The trick is simple!
The steps are :
- Draw a (light) circle to serve as boundary
- Draw a line across the diameter of this circle to serve as one side of the triangle
- From the 2 ends of the line drawn in step 2, produce 2 more lines, joining them at any point along the circle boundary.
- Smile! You have created a wonderful right-angled triangle true to target.
.
See the diagram 1 beside for an overview of the steps used.
Diagram 1 ===>
Try out this method and see for yourself!
Proof using a protractor or try square at angle C to verify the 900.
Enjoy yourself! Geometry is fun! :)
.
Exciting Area and Perimeter in Geometry
I suppose, you are also good at calculating their numerical value.
However, in the midst of doing the many calculations and heavily involved with different funny shapes, the fundamentals of geometry have to be maintained. The principles are always the main issue while studying mathematics. Take a thinker below.
Is perimeter related to area in any way?
Does the perimeter expands with increase in area?
Does the area shrink with decrease in perimeter?
These questions serve to address understanding of these 2 key geometrical parameters.
If you are able to answer them correctly, give yourself a pat.
Otherwise, give yourself a slap!
Let's look further into them, if you have any queries.
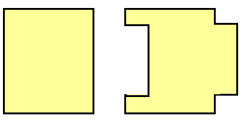
The 2 diagrams to the left has the SAME area, but look at their perimeter. One is longer than the other even when the areas are the same.
Amazing right?
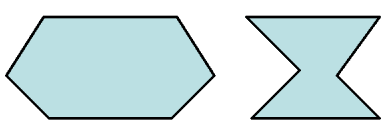
Now, look at the 2 diagrams on the left. These 2 shapes has the SAME perimeter, but how about their areas?
The areas are highly different!
Exciting area and perimeter relation, right?
Do note, however, that the above 2 cases are just to illustrate concepts of area and perimeter in geometry. There are also normal cases where increase in area results in increase in perimeter, and likewise for decreasing condition.
Stick to principles and understanding is assured. Cheers!
.
Why Is Net Important In Geometry?
The height factor of the geometrical outlook is presented in the 3-dimensional view.
But does it really present the object with a complete understanding of its shape?
There may be assumptions made if the angle of view is not appropriate.
The assumptions may be wrong!
Let me cite one example below.
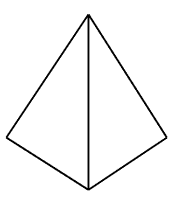
From looking at the shape presented on the left, can you tell whether the shape is that of a tetrahedron or pyramid?
Rather difficult isn't it?
It is almost impossible to tell!
Therefore, NET comes in useful in this aspect.
So, what is this net about?
Net is a different way of presenting shape. It utilises only 2-dimensional view. It is actually a 3-D object "flattened" into 2-D perspective.
The usefulness of net can be seen from the answer it presents below using the above object as reference.
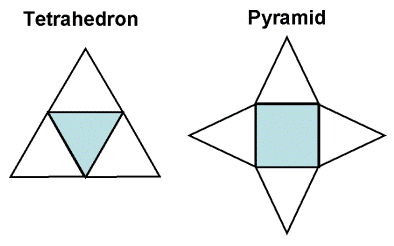
Here, if the net of the object is shown, as compared to its 3-D version, the message is clearly presented.
If the object is a tetrahedron, then the net is that of the left.
If the object is a pyramid, then the net is that of the right.
Thus, net in geometry serves its purpose in showing a clearer idea of shape when the 3-D perspective is not sufficient to reveal all details.
One common application of net is in ORIGAMI, an interesting paper folding activity liked by many.
:)
How Fast Can Spiderman Get Freedom? | A tricky question
You need to read the question, understand it, and think carefully about it.
Do not be afraid, though.
It is only applicable for fun or amusement.
I have one here. * Dare to attempt... ? *
Question:
Spiderman fell into a deep and slippery oil tunnel dugg vertically into the ground. To get out into the city, he has to, obviously, climb out of it. However, the tunnel is 20 metres deep, and he can only manage to move up 3 metres per hour due to back injury. But as the wall of the tunnel is too slippery, any attempt to move 3 metres will result in a slip back of 2 metres. This make spiderman's rate of climb to be effectively pegged at 1 metre per hour only. How long will spiderman then take to reach out of the tunnel?
NOTE: It seems like spiderman needs take 20 hours to achieve this feat. This is due to the tunnel height of 20 metres and his rate of upward climb being at 1 metre / hour. This is wrong! The assumption has to be properly thought over. Spiderman will be happy as it will take lesser time for him to reach freedom.
....... think it over, if you surrender and urgently need to see spiderman .......
.
the answer is ==>
Spiderman will be over the edge of the tunnel at the " see below " hours.
Why?
As he can only progress at 1 metre / hour, it meant that at the 2th hour, he will only start at a 2 metre height from bottom. At the 18th hour, he will start at 18 metres from bottom. From there on, he just need to cover another 2 metres to be over the edge of the tunnel (before falling back 2 metres). Therefore he needs only 18 hours plus another 2/3 hour to be happy. Got it?
:D
Principle of Speed Calculation
The question asked about the time taken when two persons or cars travelling at different speed and opposite direction meet each other.
A quick way to solve this question for its time is to apply the below:
Time taken = Total distance between the two objects / Total sum of the two speeds
However, what if we forgot this so-called formula?
As Albert Einstein once said "Education is what is left after all else is forgotten".
This is very true in learning, especially for maths.
If you forgot the formula to a question and without understanding its concepts and principles, do you think you can solve that question?
Yes, only by accident, if you are lucky.
Understanding the principles is very important as it enables you to solve any question starting from basic if all else has been "returned to the teacher".
Let us look at an example.
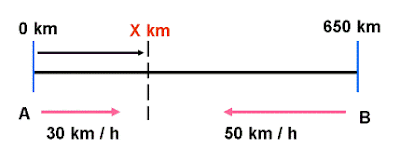
If 2 cars travelling at the speed of 30 km/h and 50 km/h meet at a distance X km away from the starting point of A, what is the time they will meet if they start off at the same time? The distance between them is 650 km apart.
Quick way to solve: T = 650 / (30 + 50) = 650 / 80 = 8.125 hrs (from start time).
From first principle:
Let the distance they meet be X km (from A point).
Since the time they meet is the same from A and B starting points,
X / 30 = (650 - X) / 50 ==> To find the value of X
(X / 30) + (X /50) = 650 /50 = 13
(50X + 30X) / 1500 = 13
80X = 1500 times 13 = 19500 ===> X = 19500 / 80 = 240.375 km
Time taken (T) for them to meet = X / 30 = 8.125 hrs (from start time).
Look here:
T = 19500/ (30 x80) hrs or
T = (19500/30) / 80 = 650 / 80 hrs
The "650" above (in bold) isn't it equal to the distance apart between the 2 cars?
The "80" above (in bold) isn't it equal to the total sum of the 2 speeds?
The working from first principle produces the SAME answer as the quick method!
But the major difference is that the solution from the Quick way has no long-lasting impact on learning as compared to the latter technique, which bank on understanding of principles of speed, time and distance.
Therefore, which way do you prefer (for longer retention of knowledge)?
:)
Maths Game - "Reversity"
You will find it wonderful and importantly, it is free and requires only a piece of paper and a pencil to go with it.
This activity is not new. I have seen many with deviation.
Here I will share with you the concept.
CONCEPT: The target ( a list of number from 1 to 10, or similar list) is to be produced using a set of pre-defined numbers, or a certain number only. Any mathematical operation can be utilised to achieve the target.
Example:
To produce a list of number from 0 to 10 using ALL the numbers 1, 2, 3 and 4, with any of the mathematics operators, + , -, /, x, ) ( and exponential.
Here it goes...
0 = 4 - 3 - ( 2 - 1 )
1 = (4 - 2 )/ (3 - 1 )
2 = (4 + 21) / 3
3 = 41 + 2 -3
4 = 4 x 2 - 3 - 1
5 = 4 x 2 - 31
6 = 4 + 2 / 13
7 = 4 + 3 / 12
8 = 4 x 2 / 13
9 = 4 x 2 + 13
10 = 4 x 2 + 3 - 1
This is a simple maths game, but it involves the application of the basic principle of mathematics to achieve the targeted number for a given set of constraints.
"Reversity" - a reversal of the mathematical procedure.
Another tougher Reversity game is to have only the number 4 used.
Any deviation can be created to generate different levels of difficulties. Explore it!
Keep your mind in reverse gear ....... ! s r e e h C (reversed)
.
Number Game To Make Maths Fun
You can play games with maths. With a bit of creativity, you can create lots of fun.
I just encountered one word game initiated by a nice member at the social site BlogCatalog .
The game started with a word (has to be more than 5 letters). The next member has to continue with another word but has to start it using the last letter of the previous word. Sort of fun going especially when you see the people whacking at the comment space to participate.
Improvise this concept to maths :
Maths Game
Make use of any 3 different maths operators to generate the number 18.
Rule of the game: The last maths operator has to be the first for the next person to continue, and no numbers in the operation are to be the same.
Start: 18 ==> 40 / 2 - 5 + 3 ==> .......
Happy thinking :D
.
Maths Concept and Its Implications
Most maths learners do face this sort of situation while learning maths. It is a learning phase in education.
What is therefore the message behind this phase?
In this phase, you will discover that purely understanding the steps or procedures in "attacking" a mathematics problem may not cover all aspect of the topic involved. Extra (hidden) elements are also mixed into the learning to form complete comprehension of the mathematics topics.
What normally is the strategy maths teacher use to teach, especially in a classroom setting, is to "drill" students into mastering a topic, practising till the idea goes into the head. It is an effective way to transfer knowledge, but with limitation.
Students are left, sometimes, to figure out the underlying concepts themselves. This is so due to many factors, examples like time resources, ability of the class to understand details, teaching style, and assumptions on the part of students and teachers.
All these contributed to gray areas in the learning of maths, thus producing gaps in the knowledge acquiring process.
What is a better way to handle maths in a classroom learning environment?
Do not blame. Take learning to be a personal challenge to be guided by the teacher. There are always too many factors in class to handle, and some aspect of learning and teaching will definitely be missed out, especially when different students has different aptitude towards maths.
After all, you, the maths student, is the one who is learning and aiming to be better, not the teacher!
What you can do with in maths learning is the understanding of maths concept as opposed to ability to solve rigid questions step-by-step. (You can solve many similar types of maths problems but still do not know its concepts - this is not true learning).
Let me cite a few examples to illustrate the "concept" element.
Example 1:
Finding the area of a given triangle with known height and base.
Formula is Area = (1/2) x Height x Base length.
Yes, you can calculate the area from the formula and given information.
If we give you another triangle with the SAME information but slanted in angles. What is the approach?
For those who did not master the geometrical area concept, they will start off with the calculation as usual, and obtaining an answer that is correct in number.
For those who had mastered the underlying area concept, they will know that the area calculation is not necessary, and the answer will be the same as previous. This is so since the area formula spells out clearly that angles of the triangle has no relation with the area computation. (Even if they showed the workings, they reflect it to get marks for the steps).
The two styles of learning, therefore, clearly, showed the strength in the latter case as it allows you to grasp an overall understanding of area. You are not mechanically drilled into rigid step-by-step solving. You are elevated into "flexible" application of concept at a higher learning platform when you practise the latter technique. You are able to link with a bigger picture in mind.
Example 2:
Solve 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 = ?
If you understand the concept of "Multiply", you will solve the question efficiently.
(Solution: 8 x 8 = 64 , short and sweet)
You can, however, solve this the rigid way by adding up all the "8"s also, but, is this the proper method when you already know of a better technique?
Example 3:
Simplify log3 X + log3 Y into a single logarithmic term.
You can solve this by applying the logarithmic Product formula to get an answer of log3 XY.
But what if the question changes to 1 + log3 X ?
Without understanding the Product concept, you will be stuck!
Why?
Product concept in logarithm calls for terms to be expressed in the "log" form for proper combination later.
(Solution: 1 has to be changed to log3 3 to be able to continue).
Therefore ways has to be found or linked to previous knowledge to capture another "log" term for the "1" in the new maths question to simplify the problem.
The above three examples, hopefully, demonstrated the importance of comprehending concepts (the extra hidden element) to reap effective learning. This addresses the issue of solving ANY mathematics questions regardless of how they are asked and how they are twisted.
The implication of studying with mastery of concepts in mind has far-reaching advantages in your future endeavours as it allows you to have the "flexible" approach to problem-solving in an effectiveness manner.
:P
How Many Decimal Places To Use?
"How many decimal places have I to use for this computing?".
This is not a simple question to answer.
Though the teacher may simply say "Use 3 decimal places" as a yardstick or to standardise marking or solutions, what is the underlying importance of selecting the correct amount of decimal places?
Many a times, the number of decimal places to be used in any mathematical calculation is not significant at elementary maths level. What is required at that education level is the understanding of the maths working or steps in solving the maths questions.
However, as we progress up the educational ladder, the importance or precision of the answer becomes significant.
Let us look at one example and its impact.
Example A: 2.143 has 2 parts.
- 1st part is the integral portion of "2"
- 2nd part is the 3 decimal places for "143" (after the decimal point).
Now let's divide the number 4 by the number in example A, and see the effect to the answer when we select various number of decimal places.
1) 4 / 2.143 = 1.867
2) 4 / 2.14 = 1.869
3) 4 / 2.1 = 1.905
What do you see in these results?
Not much changes right?
This is because the number divided "4" is too near or of the same unit as the divisor.
Let's change the number to be divided to 40.
1) 40 / 2.143 = 18.67
2) 40 / 2.143 = 18.69
3) 40 / 2.1 = 19.05
Do you notice that the difference got bigger?
What is the impact when the number to be divided increases to 400?
The differences will be drastic now!
400/ 2.143 = 186.7 and 400 /2.1 = 190.5, a difference of 3.8!
So what's the rationale in deciding the number of decimal places?
We need to understand the relative scale of all the numbers involved in the computation of the maths questions.
When the numbers involved are of the same scale, the number of decimal places is not an issue. However, when numbers are relatively bigger, more decimal places are required to have better precision to reflect an accurate answer.
In the last division, it may be a difference of 3.8 metre of length or $3.8 difference in monetary change!
Maths learning, thus, not only involves pure manual calculation, but also involves the logical interpretation of the steps and the impact of the numbers and their decimal placement.
The logical thinking part in maths education does places a significant benefit to anyone mastering maths in his future life, as he is able to decide and use the appropriate method and techniques to achieve results.
.