They are however done in another interesting way.
This is so since a matrix consists of a set of numbers within it.
Therefore multiplying matrices are not so straight forward as normal numbers.
But do rest assure that there is nothing new, it is still simple multiplication ( and addition / subtraction).
Maths is simple and interesting, remember? Read on for the steps and caution points.
Below I show multiplication using 2 matrices of the 2 x 2 order.
Do note that I have presented the steps first, leaving out the technical computation later on in this post (below the diagram).
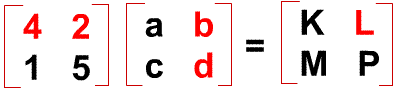
See below for the steps:
- element "K" is obtained from the first row of left matrix and the first column of the next matrix,
- element "L" is obtained using first row of left matrix and SECOND column f next matrix.
- element "M" is obtained using SECOND row of left matrix and first column of next matrix.
- element "P" is using second row and column of the respective matrices.
These sequence is of utmost importance. Why?
By not following the sequence to obtain the final elements, the numbers will be simply messed up! This is a very common mistake among students of matrices.
It is mental discipline to systematically derive the elements in the appropriate positions.
Next, let us go into getting the actual number for the final elements. Here we go...
Elements "K" = (4 x a) + (2 x c)
Element "L" = (4 x b) + (2 x d)
Element "M" = (1 x a) + (5 x c)
Element "N" = (1 x b) + (5 x d) ===> There is it, you have gotten all the elements!
There is nothing difficult, right? Matrix study is one of the simplest topics in maths.
Have fun!
.
+copy.jpg)







No comments:
Post a Comment