Monday, 29 September 2008
Is Maths Fearful?
Everyone is frighten of something. Everyone has "likes" and "don't likes".
We are human. We have emotion, temperament and preferences.
Knowing that, you are in the correct path to math learning.
What is so fearful about maths?
Or rather why are you frighten of a particular thing?
We are frighten of certain things because, we are simply, not in control of that thing.
We do not know when it will come, or when will it happen.
When it occurs, we are not able to handle it.
So you see the problem now?
Now that you see the problem or problems, the next step is to resolve them. Logical, right?
Let's for here, focus on this maths issue.
Maths, when you really look at it, does not have any fantastic things within it.
What it has is the normal numbers, symbols, equations, formula, etc. Nothing great.
What is fearful is the relationship between all the elements.
Handling relationship is always a tricky problem, similarly to human matters.
Therefore, identify which part of this relation you have trouble with.
Is it that you forgot the meaning of the symbol, thus resulting in non-linking of the equation?
Is it technique of solving that poses an obstacle? The relationship of method to expression?
Learn to solve this maths hiccups and untangle the knots. Rid yourself of the "fear", that is apparently when you are not in control.
Control your learning. Pay attention to the math teacher. Do your assignment properly. Do not copy answers. Seek for understanding.
These are a few suggestions that I can present here for your reference, and hopefully, twist your fear for math to liking math.
Maths is not that difficult. It is just a subject to test our mind only.
:-)
We are human. We have emotion, temperament and preferences.
Knowing that, you are in the correct path to math learning.
What is so fearful about maths?
Or rather why are you frighten of a particular thing?
We are frighten of certain things because, we are simply, not in control of that thing.
We do not know when it will come, or when will it happen.
When it occurs, we are not able to handle it.
So you see the problem now?
Now that you see the problem or problems, the next step is to resolve them. Logical, right?
Let's for here, focus on this maths issue.
Maths, when you really look at it, does not have any fantastic things within it.
What it has is the normal numbers, symbols, equations, formula, etc. Nothing great.
What is fearful is the relationship between all the elements.
Handling relationship is always a tricky problem, similarly to human matters.
Therefore, identify which part of this relation you have trouble with.
Is it that you forgot the meaning of the symbol, thus resulting in non-linking of the equation?
Is it technique of solving that poses an obstacle? The relationship of method to expression?
Learn to solve this maths hiccups and untangle the knots. Rid yourself of the "fear", that is apparently when you are not in control.
Control your learning. Pay attention to the math teacher. Do your assignment properly. Do not copy answers. Seek for understanding.
These are a few suggestions that I can present here for your reference, and hopefully, twist your fear for math to liking math.
Maths is not that difficult. It is just a subject to test our mind only.
:-)
Labels:
Learning maths
Thursday, 25 September 2008
How To Transpose A Matrix
Transposing a matrix is a term for a process that "swap" the row of a matrix with its column.
All the elements within the matrix remain except for their placement.
NOTE: Matrix transpose is important and a key step in getting the Inverse matrix which is required in the solving of simultaneous equations.
The procedure to transpose is simple, but saying that, caution has to be taken of which direction to "rotate". Look carefully at the coloured elements to see the direction (below diagram).

Here you see that the symbol to represent "Transpose" s the "T" besides the original matrix. The elements remain intact and not shifted yet.
Only upon transposing, the "T" disappeared.
Now, see how the transposed elements are done.
The first row is changed to the first column, with the element "a" being the pivot point.
Common mistake:
The pivot point (element) is taken wrongly. Normally element "c" is the target which is incorrect!
Stay focus when doing this transpose. You will then rid yourself of less trouble.
Cheers! Remember, maths is interesting! (If you are doing the correct thing.)
.
All the elements within the matrix remain except for their placement.
NOTE: Matrix transpose is important and a key step in getting the Inverse matrix which is required in the solving of simultaneous equations.
The procedure to transpose is simple, but saying that, caution has to be taken of which direction to "rotate". Look carefully at the coloured elements to see the direction (below diagram).

Here you see that the symbol to represent "Transpose" s the "T" besides the original matrix. The elements remain intact and not shifted yet.
Only upon transposing, the "T" disappeared.
Now, see how the transposed elements are done.
The first row is changed to the first column, with the element "a" being the pivot point.
Common mistake:
The pivot point (element) is taken wrongly. Normally element "c" is the target which is incorrect!
Stay focus when doing this transpose. You will then rid yourself of less trouble.
Cheers! Remember, maths is interesting! (If you are doing the correct thing.)
.
Labels:
matrices
Wednesday, 24 September 2008
How to do the 3 x 3 order determinant using Rule of Sarrus
It is very often that we come across the word determinant in matrices. Yes, they are related.
Matrix consists a set of numbers. That's it.
Determinant is a numerical value obtained throught the numbers within the matrix.
For a 3 x 3 matrix, how then do we extract the determinant?
One of the easiest method to obtain this number is throught the use of Rule of Sarrus.
Below I show the steps.

Determinant A = [(aei) + (bfg) + (cdh) ] - [ (gec) + (hfa) + (idb) ].
=====================================================>>>
The important step lies with getting the first left 2 columns out to the right of the determinant.
After which, we do a downwards grouping and addition.
This is followed by upwards grouping with addition again.
Note, the last step is to SUBTRACT the two groups obtained above.
(By grouping, I mean to MULTIPLY the individual elements).
Common mistakes:
1) The grouping is done by "adding" instead of multiplying the elements.
2) The slanted operations (the 3 element-multiplication) are done by "adding" instead of multiplying the 3 elements.
3) The two big groups are "added" instead of subtracted".
Just bear in mind the 3 common mistakes above and you are on the way to a happy matrix student...
Cheers!
Matrix consists a set of numbers. That's it.
Determinant is a numerical value obtained throught the numbers within the matrix.
For a 3 x 3 matrix, how then do we extract the determinant?
One of the easiest method to obtain this number is throught the use of Rule of Sarrus.
Below I show the steps.

Determinant A = [(aei) + (bfg) + (cdh) ] - [ (gec) + (hfa) + (idb) ].
=====================================================>>>
The important step lies with getting the first left 2 columns out to the right of the determinant.
After which, we do a downwards grouping and addition.
This is followed by upwards grouping with addition again.
Note, the last step is to SUBTRACT the two groups obtained above.
(By grouping, I mean to MULTIPLY the individual elements).
Common mistakes:
1) The grouping is done by "adding" instead of multiplying the elements.
2) The slanted operations (the 3 element-multiplication) are done by "adding" instead of multiplying the 3 elements.
3) The two big groups are "added" instead of subtracted".
Just bear in mind the 3 common mistakes above and you are on the way to a happy matrix student...
Cheers!
Labels:
matrices
Monday, 22 September 2008
Curious Maths Terms
Have some fun with the terms used in maths...
1) Doing multiplication without tables ===> Doing the maths problems on the floor
2) Using integration ===> Discussing with classmates and copying relevant answers
3) Using differentiation ===> Sorting out what can be done and what can't
4) Finding partial fractions ===> allowed to complete the computation partially
5) Calculating standard deviation ===> finding out how many more marks to hit standard pass grade
Caution:
Do not take this too serious, otherwise ....... you will really have to check your standard deviation.
.
1) Doing multiplication without tables ===> Doing the maths problems on the floor
2) Using integration ===> Discussing with classmates and copying relevant answers
3) Using differentiation ===> Sorting out what can be done and what can't
4) Finding partial fractions ===> allowed to complete the computation partially
5) Calculating standard deviation ===> finding out how many more marks to hit standard pass grade
Caution:
Do not take this too serious, otherwise ....... you will really have to check your standard deviation.
.
Labels:
Fun in maths
Wednesday, 17 September 2008
Multiplication of Matrices
As do normal number multiplication, matrices themselves, also have their set of multiplication.
They are however done in another interesting way.
This is so since a matrix consists of a set of numbers within it.
Therefore multiplying matrices are not so straight forward as normal numbers.
But do rest assure that there is nothing new, it is still simple multiplication ( and addition / subtraction).
Maths is simple and interesting, remember? Read on for the steps and caution points.
Below I show multiplication using 2 matrices of the 2 x 2 order.
Do note that I have presented the steps first, leaving out the technical computation later on in this post (below the diagram).
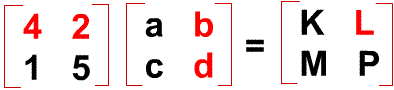
See below for the steps:
.
They are however done in another interesting way.
This is so since a matrix consists of a set of numbers within it.
Therefore multiplying matrices are not so straight forward as normal numbers.
But do rest assure that there is nothing new, it is still simple multiplication ( and addition / subtraction).
Maths is simple and interesting, remember? Read on for the steps and caution points.
Below I show multiplication using 2 matrices of the 2 x 2 order.
Do note that I have presented the steps first, leaving out the technical computation later on in this post (below the diagram).
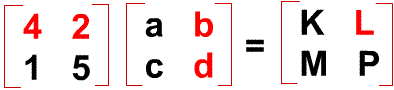
See below for the steps:
- element "K" is obtained from the first row of left matrix and the first column of the next matrix,
- element "L" is obtained using first row of left matrix and SECOND column f next matrix.
- element "M" is obtained using SECOND row of left matrix and first column of next matrix.
- element "P" is using second row and column of the respective matrices.
These sequence is of utmost importance. Why?
By not following the sequence to obtain the final elements, the numbers will be simply messed up! This is a very common mistake among students of matrices.
It is mental discipline to systematically derive the elements in the appropriate positions.
Next, let us go into getting the actual number for the final elements. Here we go...
Elements "K" = (4 x a) + (2 x c)
Element "L" = (4 x b) + (2 x d)
Element "M" = (1 x a) + (5 x c)
Element "N" = (1 x b) + (5 x d) ===> There is it, you have gotten all the elements!
There is nothing difficult, right? Matrix study is one of the simplest topics in maths.
Have fun!
.
Labels:
matrices
Thursday, 11 September 2008
Math Challenge (10)
It is time for us to play some math game.
You do not need a university degree to handle this game.
Everyone can play. It is meant to exercise your brain, nothing taxing.
What is this game about?
Challenge
There is a series of numbers that you have to add mathematical operators (+, -, / , x or brackets) to. The addition of these operators has to satisfy the end result though.
Example:
2 2 2 2 = 0 => Solution is 2 + 2 - 2 - 2 = 0
2 2 2 2 = 1
2 2 2 2 = 2
2 2 2 2 = 3
2 2 2 2 = 4
2 2 2 2 = 5
2 2 2 2 = 6
2 2 2 2 = 7
2 2 2 2 = 8
2 2 2 2 = 9
Nothing difficult, right? It is just to get your brain moving, otherwise it will go rusty.
Enjoy yourself.
You may also alter the list to include other numbers.
4 4 5 5 = 1
4 4 5 5 = 2
4 4 5 5 = 3
and so on .......
:-)
You do not need a university degree to handle this game.
Everyone can play. It is meant to exercise your brain, nothing taxing.
What is this game about?
Challenge
There is a series of numbers that you have to add mathematical operators (+, -, / , x or brackets) to. The addition of these operators has to satisfy the end result though.
Example:
2 2 2 2 = 0 => Solution is 2 + 2 - 2 - 2 = 0
2 2 2 2 = 1
2 2 2 2 = 2
2 2 2 2 = 3
2 2 2 2 = 4
2 2 2 2 = 5
2 2 2 2 = 6
2 2 2 2 = 7
2 2 2 2 = 8
2 2 2 2 = 9
Nothing difficult, right? It is just to get your brain moving, otherwise it will go rusty.
Enjoy yourself.
You may also alter the list to include other numbers.
4 4 5 5 = 1
4 4 5 5 = 2
4 4 5 5 = 3
and so on .......
:-)
Labels:
Maths Thinker
Sunday, 7 September 2008
Matrices | What is Minor?
Before you read this, say "maths is interesting!". Mental trick....
Now you may start.
In matrices, there is an important basic term residing in it.
It is the term called "minor" and is obtained through the determinant of the matrix.
For 2nd order matrix (or determinant), there will be 4 minors since there are 4 elements within the determinant.
For 3rd order form, there will inevitably, be 9 minors.
To have an idea what "order of matrix" is about, go to this link here.
How to compute this minor?
See below...
The method is simple, right?
It involves the correct cancellation of the appropriate row and column.
The leftover elements will be used to determine the value.
To enhance understanding, let's do another example.Find the minor of element 2.
The leftover is the elements
4 6
7 9
The determinant value of the leftover is then (4)(9) - (7)(6) = 36 - 42 = -6.
This is the minor for element "2".
Common mistake made:
The minor is always taken as the actual element in question.
Example of mistakes:
To find the minor of element "2" in the above determinant
==> Wrong answer = "2", the original element used to get the leftover after cancellation.
To find the minor of element "1" in the above determinant
==> Wrong answer = "1", the original element used to get the leftover after cancellation.
NOTE:
Minor and Co-factor are closely related. They are needed to compute Adjoint and Inverse matrix.
You have to master these concepts to be able to handle matrices.
Tough, right? If your answer is YES, you are wrong!
Look and review the above methods again, and you will be sure that they are simply +, _, x only.
Isn't this what you have been learning since lower elementary?
:-)
Now you may start.
In matrices, there is an important basic term residing in it.
It is the term called "minor" and is obtained through the determinant of the matrix.
For 2nd order matrix (or determinant), there will be 4 minors since there are 4 elements within the determinant.
For 3rd order form, there will inevitably, be 9 minors.
To have an idea what "order of matrix" is about, go to this link here.
How to compute this minor?
See below...
The method is simple, right?
It involves the correct cancellation of the appropriate row and column.
The leftover elements will be used to determine the value.
To enhance understanding, let's do another example.Find the minor of element 2.
The leftover is the elements
4 6
7 9
The determinant value of the leftover is then (4)(9) - (7)(6) = 36 - 42 = -6.
This is the minor for element "2".
Common mistake made:
The minor is always taken as the actual element in question.
Example of mistakes:
To find the minor of element "2" in the above determinant
==> Wrong answer = "2", the original element used to get the leftover after cancellation.
To find the minor of element "1" in the above determinant
==> Wrong answer = "1", the original element used to get the leftover after cancellation.
NOTE:
Minor and Co-factor are closely related. They are needed to compute Adjoint and Inverse matrix.
You have to master these concepts to be able to handle matrices.
Tough, right? If your answer is YES, you are wrong!
Look and review the above methods again, and you will be sure that they are simply +, _, x only.
Isn't this what you have been learning since lower elementary?
:-)
Labels:
matrices
How To Get Determinant Value
In the study of matrices, you will come across the computation of determinant and their values.
These determinants come in various order.
There are the 2nd order, 3rd order, and so on.
What is this order?
Order is the number of rows and column within the determinant.
Thus, 2nd order determinant has 2 rows and 2 columns.
3rd order has 3 rows and 3 columns.
To calculate the values of these determinants, see below for the methods.

The 2nd order is shown in the first upper line.
Following that is the 3rd order computation, using the special Rule of Sarrus (the simpler form of 3rd order calculation).
This value computed comes in useful to determine other values.
One of the examples is the solution of simultaneous equations and their unknowns.
The technique presented here is thus, basic knowledge in matrices learning.
These determinants come in various order.
There are the 2nd order, 3rd order, and so on.
What is this order?
Order is the number of rows and column within the determinant.
Thus, 2nd order determinant has 2 rows and 2 columns.
3rd order has 3 rows and 3 columns.
To calculate the values of these determinants, see below for the methods.

The 2nd order is shown in the first upper line.
Following that is the 3rd order computation, using the special Rule of Sarrus (the simpler form of 3rd order calculation).
This value computed comes in useful to determine other values.
One of the examples is the solution of simultaneous equations and their unknowns.
The technique presented here is thus, basic knowledge in matrices learning.
Labels:
matrices
Saturday, 6 September 2008
Adjoint and Inverse Matrix } Their relationship
There is a common misunderstanding among math learners over the common term in matrices.
The two terms are the Adjoint and Inverse matrix.
The operation to get them is somewhat always confused and "mixed up".
Here to clear and simplify their differences:
- Adjoint matrix
It is obtained through the co-factors of each elements within the matrix. After which the matrix is transposed. It stops there.
- Inverse matrix
The adjoint matrix forms part of this inverse matrix!
Inverse matrix needs a further computation of the determinant also.
The final outcome is the adjoint matrix divided by this determinant value.
Therefore in summary, inverse matrix is formed out of the adjoint matrix.
They are husband and wife, with the kids, the minor and co-factors in them.
.
The two terms are the Adjoint and Inverse matrix.
The operation to get them is somewhat always confused and "mixed up".
Here to clear and simplify their differences:
- Adjoint matrix
It is obtained through the co-factors of each elements within the matrix. After which the matrix is transposed. It stops there.
- Inverse matrix
The adjoint matrix forms part of this inverse matrix!
Inverse matrix needs a further computation of the determinant also.
The final outcome is the adjoint matrix divided by this determinant value.
Therefore in summary, inverse matrix is formed out of the adjoint matrix.
They are husband and wife, with the kids, the minor and co-factors in them.
.
Labels:
matrices
Subscribe to:
Posts (Atom)

+copy.jpg)






