Wednesday, 31 December 2008
Mistake with A^2 - B^2
In algebra, a very common mistake you can see learner making is the below:
52 - 22 = (5 - 2)2 = 32 = 9
This is very interesting.
It seems to be correct. That is the problem with this form of mathematical operation.
If you are aware that A2 - B2 = (A + B)(A - B), then this mistake will not occur.
It is this slip-of-the-mind type of human error.
It occurs when you are not alert or too tired after too many assignment quesions.
The correct answer is 52 - 22 = 25 - 4 = 21.
Or (5 + 2)(5 - 2) = 7 x 3 = 21.
Simple?
This is why maths is interesting. It catches you when you are not alert!
.
52 - 22 = (5 - 2)2 = 32 = 9
This is very interesting.
It seems to be correct. That is the problem with this form of mathematical operation.
If you are aware that A2 - B2 = (A + B)(A - B), then this mistake will not occur.
It is this slip-of-the-mind type of human error.
It occurs when you are not alert or too tired after too many assignment quesions.
The correct answer is 52 - 22 = 25 - 4 = 21.
Or (5 + 2)(5 - 2) = 7 x 3 = 21.
Simple?
This is why maths is interesting. It catches you when you are not alert!
.
Labels:
Algebra,
mistakes,
principles
Monday, 29 December 2008
Key Differences Between Cos and Log Operations
It has been mentioned in previous posts that "cos" and "log" are actually mathematical operators.
They cannot exist alone. They need partners.
For "cos", it needs angle.
For "log", it requires a number.
They operate on something.
So what is their difference since they are both operators?
"cos" changes angle information to number (ratio).
"log" operates on number to get another number.
Their applications, thus, differ in the above matter.
NOTE: "cos" here refers to any trigonometrical functions.
"cos" is useful in getting length or angle information.
"log" can be used to find the value of the power needed.
Example: To find 2x = 5
Knowing the various mathematical tools, we can apply the correct ones to solve specific problems.
Without understanding the underlying usage and concepts, we will be at a lost to which tools to use.
Math is, therefore, wider in nature than just calculation.
Keep learning....
:-)
They cannot exist alone. They need partners.
For "cos", it needs angle.
For "log", it requires a number.
They operate on something.
So what is their difference since they are both operators?
"cos" changes angle information to number (ratio).
"log" operates on number to get another number.
Their applications, thus, differ in the above matter.
NOTE: "cos" here refers to any trigonometrical functions.
"cos" is useful in getting length or angle information.
"log" can be used to find the value of the power needed.
Example: To find 2x = 5
Knowing the various mathematical tools, we can apply the correct ones to solve specific problems.
Without understanding the underlying usage and concepts, we will be at a lost to which tools to use.
Math is, therefore, wider in nature than just calculation.
Keep learning....
:-)
Labels:
concept,
Logarithm,
maths technique,
Trigonometry
Saturday, 27 December 2008
Math Challenge 12
Although math may seem difficult at times, proper use of its principles will render it simple to handle and use.
Here, a bit of algebraic juice can help in solving the below math challenge.
Following the pattern, you will observe a "trick" that you can make use to solve the challenge later.
22 - 12 = 3
32 - 22 = 5
62 - 52 = 11
112 - 92 = 40
The above equations are done without detailed written working, just simple mental calculation.
Challenge:
162 - 142 = ??
Do it without calculator.
What is the answer to the above? At the comment session, please.
Hmmm........ tick tock tick tock
.
Here, a bit of algebraic juice can help in solving the below math challenge.
Following the pattern, you will observe a "trick" that you can make use to solve the challenge later.
22 - 12 = 3
32 - 22 = 5
62 - 52 = 11
112 - 92 = 40
The above equations are done without detailed written working, just simple mental calculation.
Challenge:
162 - 142 = ??
Do it without calculator.
What is the answer to the above? At the comment session, please.
Hmmm........ tick tock tick tock
.
Labels:
Algebra,
Maths Thinker
Wednesday, 24 December 2008
Understanding Math Principles Helps
There are many formulae that a student has to know and sometimes remember for his studies, and applications.
How then can he capture all these necessary formulae for usage?
One way is to understand the principles and derive those required later on for usage.
Example:
In trigonometry, you will come across sine of two angles, sin (A + B).
You have memorised sin (A + B) as "sinA cosB + cosA sinB".
However, when you further need to know sin 2A, what then?
If you know and understand the principles of the sin(A + B), you can easily move on to derive the sin2A.
How?
Since you know sin (A + B), you can equate A = B, to allow you to get the sin(A + A).
As sin (A + A) = sin2A, you will then have no problem achieving
sin(A +A) = sinA cosA + cosA sinA ==> sin 2A = 2sinAcosA
There, you have obtained another formula without the need to memorise it.
Thus mastering the sin (A + B) principles or its equivalent, can allow you to expand your knowledge further.
You see the benefits now?
I have shown only the trigonometry part in math learning, but, you can appreciate that it applies to any other topics as well.
Seek, therefore to handle principles of math well as it will serve you good in the long run.
:-) ..... :-) Forever liking mathematics. Maths is interesting!
.
How then can he capture all these necessary formulae for usage?
One way is to understand the principles and derive those required later on for usage.
Example:
In trigonometry, you will come across sine of two angles, sin (A + B).
You have memorised sin (A + B) as "sinA cosB + cosA sinB".
However, when you further need to know sin 2A, what then?
If you know and understand the principles of the sin(A + B), you can easily move on to derive the sin2A.
How?
Since you know sin (A + B), you can equate A = B, to allow you to get the sin(A + A).
As sin (A + A) = sin2A, you will then have no problem achieving
sin(A +A) = sinA cosA + cosA sinA ==> sin 2A = 2sinAcosA
There, you have obtained another formula without the need to memorise it.
Thus mastering the sin (A + B) principles or its equivalent, can allow you to expand your knowledge further.
You see the benefits now?
I have shown only the trigonometry part in math learning, but, you can appreciate that it applies to any other topics as well.
Seek, therefore to handle principles of math well as it will serve you good in the long run.
:-) ..... :-) Forever liking mathematics. Maths is interesting!
.
Labels:
concept,
Learning maths,
principles,
Trigonometry
Monday, 22 December 2008
Math Challenge 11
What is the simplest way to solve the below equation?
cos X = log X.
You may wish to give your suggestions in the comment space.
Hints:
1) There are 3 answers to the above relation.
2) Sometimes technique not related to logarithm or trigonometry can be useful.
Happy thinking ....... (:-)
.
cos X = log X.
You may wish to give your suggestions in the comment space.
Hints:
1) There are 3 answers to the above relation.
2) Sometimes technique not related to logarithm or trigonometry can be useful.
Happy thinking ....... (:-)
.
Labels:
Maths Thinker
Saturday, 20 December 2008
Mistake in Cos(A + B)
We do encounter question like,
"Find the angle of A in cos (A + 45) = 0.42 ".
What do you do?
Two solutions are presented as below:
Solution 1:
cos (A + 45) = 0.42
==> A + 45 = cos-1 0.42
==> A = 65.17 - 45 = 20.17 (Answer)
Solution 2:
cosA + cos45 = 0.42
==> cosA = 0.42 - 0.707 = - 0.287
==> A = cos-1(-0.287)
==> A = 106.69 (Answer)
You can see that the 2 answers are different.
Why? Or is there 2 valid answers?
Looking carefully at the solutions above, you will see two concepts in approaching the solving.
The first working went through the conventional inverse cosine operation using the summed up angle (A + 45) as a piece.
The second solution used the concept of algebraic factorising to split the angles A and 45 before processing them separately.
What is wrong here?
To reveal the answer in advance, the first solution is correct while the second has a common mathematical fault.
cos (A + 45) means an operation of cosine onto the angles (A + 45) as a whole.
"cos" is not a variable to be operated upon.
Therefore, "cos" cannot be factorised!
The step, cos (A + 45), cannot be equal to cosA + cos45.
This is a common mistake that need to be removed from the brain.
Press the "Delete" button.
With this post, your trigonometry is getting better right?
Cheers!
You may visit this post for more mistakes to be avoided.
;)
"Find the angle of A in cos (A + 45) = 0.42 ".
What do you do?
Two solutions are presented as below:
Solution 1:
cos (A + 45) = 0.42
==> A + 45 = cos-1 0.42
==> A = 65.17 - 45 = 20.17 (Answer)
Solution 2:
cosA + cos45 = 0.42
==> cosA = 0.42 - 0.707 = - 0.287
==> A = cos-1(-0.287)
==> A = 106.69 (Answer)
You can see that the 2 answers are different.
Why? Or is there 2 valid answers?
Looking carefully at the solutions above, you will see two concepts in approaching the solving.
The first working went through the conventional inverse cosine operation using the summed up angle (A + 45) as a piece.
The second solution used the concept of algebraic factorising to split the angles A and 45 before processing them separately.
What is wrong here?
To reveal the answer in advance, the first solution is correct while the second has a common mathematical fault.
cos (A + 45) means an operation of cosine onto the angles (A + 45) as a whole.
"cos" is not a variable to be operated upon.
Therefore, "cos" cannot be factorised!
The step, cos (A + 45), cannot be equal to cosA + cos45.
This is a common mistake that need to be removed from the brain.
Press the "Delete" button.
With this post, your trigonometry is getting better right?
Cheers!
You may visit this post for more mistakes to be avoided.
;)
Labels:
Algebra,
mistakes,
Trigonometry
Wednesday, 17 December 2008
Cos2A IS NOT 2CosA
A common mistake in trigonometry is the misunderstanding that cosA can be taken apart.
What is the true meaning of this "cos"?
"cos", or cosine, is actually a trigonometrical operation on an angle producing a ratio or a number.
Here, cosine is taken as a reference for this type of mistake made.
Sine and tangent are the equivalent.
You cannot take the "cos" apart from the angle A. They must exist together as a pair "cosA".
For double angle 2A, any trigonometrical operation on it will be likewise treated.
Cos2A will be an operation of cosine on this double angle 2A.
"cos" cannot be treated as a variable, standing alone.
Thus cos2A is not to be separated into "cos" "2A" or (cos)(2)(A).
With this principles, cos2A is therefore, not equal to 2cosA, since the 2A is being operated with the function "cosine".
You may wish to pump in some numbers for the angle and try for yourself this verification.
Example: cos 2(20) and 2 cos(20).
Are they really equal?
As long as you understand what is operation (or function) and operand (or the variable operated upon), you will not have any serious problem with math.
:-)
What is the true meaning of this "cos"?
"cos", or cosine, is actually a trigonometrical operation on an angle producing a ratio or a number.
Here, cosine is taken as a reference for this type of mistake made.
Sine and tangent are the equivalent.
You cannot take the "cos" apart from the angle A. They must exist together as a pair "cosA".
For double angle 2A, any trigonometrical operation on it will be likewise treated.
Cos2A will be an operation of cosine on this double angle 2A.
"cos" cannot be treated as a variable, standing alone.
Thus cos2A is not to be separated into "cos" "2A" or (cos)(2)(A).
With this principles, cos2A is therefore, not equal to 2cosA, since the 2A is being operated with the function "cosine".
You may wish to pump in some numbers for the angle and try for yourself this verification.
Example: cos 2(20) and 2 cos(20).
Are they really equal?
As long as you understand what is operation (or function) and operand (or the variable operated upon), you will not have any serious problem with math.
:-)
Labels:
Algebra,
mistakes,
Trigonometry
Saturday, 13 December 2008
Mathematical Flower For Festive Season
Since this is the end of the year, with the festive season coming, I have designed a flower through the graphical means using the mathematical expression indicated.
It is done in polar form with the x as the time base and y as the modulus (amplitude).
Happy greetings to my readers.

.
It is done in polar form with the x as the time base and y as the modulus (amplitude).
Happy greetings to my readers.

.
Labels:
graphical art
Division of x^n with y^n
Confusion does happen when you are bombarded with many numbers, exponential and its likes.
After dealing with indices, logarithm and their multiplication and division, the brain will sort of tangle up and produces weird happenings.
Take 2 examples below:
1) x^n / y^n ==> x /y
2) log x^n / log y^n ==> (log x) / (log y)
By looking at the first example, you may find nothing wrong.
Since the power "n" is similar for the numerator and denominator, you can do the normal cancellation as you do for "mx / my" = x/y.
However, something may tell you that something is amiss.
While "mx / my" is truely x / y, this is because mx means m times x.
There are "m" number of x that are ADDED up.
For x^n, it means "x" is multiplied by itself n times. (or x times x times x times x ....)
Thus x^n is not equal to xn.
The truth of "cancellation" is that since a / a = 1, and this "1" is not required to be written, the disappearance seems to be "cancellation".
Let me explain further with an example(A).
ax / ay = (a/a)(x/y) = (1) (x / y) = x / y. The "1" disappeared and seems to be cancelled off.
The mistake made in Example 1 in the beginning, is the assumption that the powers "n" followed the concept of "ax" in example(A).
Correct answer for x^n / y^n = (x/y)^n. ==> The powers of n are not removed.
Now for the Example 2, at the beginning, it showed a similar cancellation of the powers "n".
But this time round, it can be said to be conditionally correct.
Why?
If the idea that similar "letter" of "n" in the power can be removed through cancellation, then the answer, although correct, is theoretically wrong.
However, if you know that using the Power Law of logarithm, log x^n can become "nlogx" and therefore, log y^n can also be "nlog y", the result of (log x) /(log y) can be rightfully considered correct, since the "n" is removed according to the idea that n/n = 1 and disappeared, or qualified for removal.
In summary, mistakes do happen when the concept of power (x^n) and pure multiplication (x times n) is not clearly understood.
Cancellation of "letters" or symbols in math expressions should be highlighted as a shortcut to removal due to being "1" that can be omitted in the written form.
This concept of "cancellation" is easy if you understand that it is because of a/a = 1.
.
After dealing with indices, logarithm and their multiplication and division, the brain will sort of tangle up and produces weird happenings.
Take 2 examples below:
1) x^n / y^n ==> x /y
2) log x^n / log y^n ==> (log x) / (log y)
By looking at the first example, you may find nothing wrong.
Since the power "n" is similar for the numerator and denominator, you can do the normal cancellation as you do for "mx / my" = x/y.
However, something may tell you that something is amiss.
While "mx / my" is truely x / y, this is because mx means m times x.
There are "m" number of x that are ADDED up.
For x^n, it means "x" is multiplied by itself n times. (or x times x times x times x ....)
Thus x^n is not equal to xn.
The truth of "cancellation" is that since a / a = 1, and this "1" is not required to be written, the disappearance seems to be "cancellation".
Let me explain further with an example(A).
ax / ay = (a/a)(x/y) = (1) (x / y) = x / y. The "1" disappeared and seems to be cancelled off.
The mistake made in Example 1 in the beginning, is the assumption that the powers "n" followed the concept of "ax" in example(A).
Correct answer for x^n / y^n = (x/y)^n. ==> The powers of n are not removed.
Now for the Example 2, at the beginning, it showed a similar cancellation of the powers "n".
But this time round, it can be said to be conditionally correct.
Why?
If the idea that similar "letter" of "n" in the power can be removed through cancellation, then the answer, although correct, is theoretically wrong.
However, if you know that using the Power Law of logarithm, log x^n can become "nlogx" and therefore, log y^n can also be "nlog y", the result of (log x) /(log y) can be rightfully considered correct, since the "n" is removed according to the idea that n/n = 1 and disappeared, or qualified for removal.
In summary, mistakes do happen when the concept of power (x^n) and pure multiplication (x times n) is not clearly understood.
Cancellation of "letters" or symbols in math expressions should be highlighted as a shortcut to removal due to being "1" that can be omitted in the written form.
This concept of "cancellation" is easy if you understand that it is because of a/a = 1.
.
Monday, 8 December 2008
Correct Method over Correct Answer
In math, you do not go for correct answer.
Yes, correct answer motivates. It is the ultimate goal for any math learner.
But is that all to math?
Math calls for more than that.
Read this story before moving on......
You have to ensure that the correct answer is gotten with the correct method and concept or principles.
Many a times, students can obtain correct answers to a math question, if it is not properly though over by the teacher.
If the teacher did not do a scrutiny over the working, the answer may be passed off as correct.
This is disaster.
If the student did not master the concept properly, this sort of happening will also results in learning disaster.
Therefore, seek to learn the correct technique or math method instead of aiming for the answer.
It is better to get wrong answer with the correct method than getting correct answer with wrong technique.
This makes learning math interesting!
.
Yes, correct answer motivates. It is the ultimate goal for any math learner.
But is that all to math?
Math calls for more than that.
Read this story before moving on......
You have to ensure that the correct answer is gotten with the correct method and concept or principles.
Many a times, students can obtain correct answers to a math question, if it is not properly though over by the teacher.
If the teacher did not do a scrutiny over the working, the answer may be passed off as correct.
This is disaster.
If the student did not master the concept properly, this sort of happening will also results in learning disaster.
Therefore, seek to learn the correct technique or math method instead of aiming for the answer.
It is better to get wrong answer with the correct method than getting correct answer with wrong technique.
This makes learning math interesting!
.
Labels:
attitude,
Learning maths,
maths technique,
teaching maths
Common "log" mistake
Teacher: John, can you give the answer for X in this log X = log 6 question?
John: No problem. The value for X is simply 6.
Teacher: Correct! How did you get the answer?
John: It is easy. Just do it this way
(John wrote on the board). ==> X = (log 6) /log ==>X = 6.
Teacher: ?????
************************* What happened? ***********************
Logarithm or "log", in its abbreviated form, can be easily misunderstood.
What is this "log"?
Logarithm is an operation on a number that is the reverse of that for indexing a number.
LogaX = Y ==> aY = X
From the above relationship, you will notice that "log" itself cannot stand alone.
That means "log" must come with a number or expression.
"Log" is an operator, like the "+" or "-".
What mistake did John made?
John mis-interpreted the "log" to be a variable!
It made him transfer the "log" over the equal symbol as though it is a number (or equivalent).
the "log" is thus, separated from the "X" that it should operate upon.
A common "log" mistake was made.
Correct answer:
The answer can be obtained through logically comparison, that is,
when log X = log 6, X is simply = 6.
The question may be simple, but if the learning is improper, the concept behind it may be drastically, wrong, even though the answer can be correct.
Learn well. Maths does not call for correct answer. It is the thinking behind it.
..... :-)
John: No problem. The value for X is simply 6.
Teacher: Correct! How did you get the answer?
John: It is easy. Just do it this way
(John wrote on the board). ==> X = (log 6) /log ==>X = 6.
Teacher: ?????
************************* What happened? ***********************
Logarithm or "log", in its abbreviated form, can be easily misunderstood.
What is this "log"?
Logarithm is an operation on a number that is the reverse of that for indexing a number.
LogaX = Y ==> aY = X
From the above relationship, you will notice that "log" itself cannot stand alone.
That means "log" must come with a number or expression.
"Log" is an operator, like the "+" or "-".
What mistake did John made?
John mis-interpreted the "log" to be a variable!
It made him transfer the "log" over the equal symbol as though it is a number (or equivalent).
the "log" is thus, separated from the "X" that it should operate upon.
A common "log" mistake was made.
Correct answer:
The answer can be obtained through logically comparison, that is,
when log X = log 6, X is simply = 6.
The question may be simple, but if the learning is improper, the concept behind it may be drastically, wrong, even though the answer can be correct.
Learn well. Maths does not call for correct answer. It is the thinking behind it.
..... :-)
Friday, 5 December 2008
Interesting Facts of Factorisation in Quadratic Equation Solving
Why do you learn factorisation?
What is the importance of factorisation?
You may have these questions when you are taught this.
Factorisation is the making of an expression into the product form, that is, (....)(....)(....).
Factorisation ends with all terms in a math expression being connected with parentheses.
What for?
To solve an equation, say, a quadratic equation, you normally make the expression equal to zero.
There is a meaning to this "equal to zero".
Using factoring method, (....)(....) = 0, implies that either one of the (..) can be zero.
Click this link for an explanation to the above statement.
This is will not be so when the terms are in the form A + B = 0 (sum format).
Factorising causes a quick, simple solving of quadratic equation by having the product form to the expression.
Example :
x2 + 3x + 2 = 0
Factorising: (x + 1) (x + 2) = 0
Through factorising the quadratic equation,
you can equate (x + 1) = 0 or (x + 2) = 0.
Thus, x = -1 or x = -2.
This is made possible by factorising.
The demerit of this factorisation method, however, is that it takes time to figure out the numbers within the factors. Not all expressions can be easily changed to the factor form through simple "guessing".
NOTE: This post is talking about numbers and not matrices, which involve another concept of dealing with AB = 0.
.
What is the importance of factorisation?
You may have these questions when you are taught this.
Factorisation is the making of an expression into the product form, that is, (....)(....)(....).
Factorisation ends with all terms in a math expression being connected with parentheses.
What for?
To solve an equation, say, a quadratic equation, you normally make the expression equal to zero.
There is a meaning to this "equal to zero".
Using factoring method, (....)(....) = 0, implies that either one of the (..) can be zero.
Click this link for an explanation to the above statement.
This is will not be so when the terms are in the form A + B = 0 (sum format).
Factorising causes a quick, simple solving of quadratic equation by having the product form to the expression.
Example :
x2 + 3x + 2 = 0
Factorising: (x + 1) (x + 2) = 0
Through factorising the quadratic equation,
you can equate (x + 1) = 0 or (x + 2) = 0.
Thus, x = -1 or x = -2.
This is made possible by factorising.
The demerit of this factorisation method, however, is that it takes time to figure out the numbers within the factors. Not all expressions can be easily changed to the factor form through simple "guessing".
NOTE: This post is talking about numbers and not matrices, which involve another concept of dealing with AB = 0.
.
Labels:
Algebra
Tuesday, 2 December 2008
Meaning of AB = 0 and AB = 1
AB = 0.
The mathematical statement seems simple.
It means the multiplication of variable A and B equals zero.
Though it seems simple and direct, mistake in understanding the implication of the zero exists.
When we say AB = 0, we indirectly (and logically) deduce that A = 0 or B = 0.
This deduction is with taken regardless of what the other variable is.
When we say A = 0, B can be anything since 0 multiply "anything" = 0.
This is true vice versa for B = 0.
But what if AB = 1? or AB = x?
This is where misconception of the "logically" deduction happens.
Many maths learners assumed that since AB = 0 indicated A = 0 or B = 0,
AB=1 indicated A = 1 or B = 1 also!
This is a grave and serious mistake made.
AB= 1 does not imply A = 1 or B = 1 .
If A = "1" is true, then AB = 1 means "1" x B = 1, which is definitely false, as 1 x B = B!
Likewise when B= 1 is assumed.
Therefore the AB = 0 cannot be applied across the board to cover all else with the same deduction.
The equal to Zero has special meaning, and should not be confused with other number equated.
In summary: AB = 0 means A= 0 or B= 0 only if "= 0".
A little accurate understanding goes a long way.... in maths, especially.
:-)
The mathematical statement seems simple.
It means the multiplication of variable A and B equals zero.
Though it seems simple and direct, mistake in understanding the implication of the zero exists.
When we say AB = 0, we indirectly (and logically) deduce that A = 0 or B = 0.
This deduction is with taken regardless of what the other variable is.
When we say A = 0, B can be anything since 0 multiply "anything" = 0.
This is true vice versa for B = 0.
But what if AB = 1? or AB = x?
This is where misconception of the "logically" deduction happens.
Many maths learners assumed that since AB = 0 indicated A = 0 or B = 0,
AB=1 indicated A = 1 or B = 1 also!
This is a grave and serious mistake made.
AB= 1 does not imply A = 1 or B = 1 .
If A = "1" is true, then AB = 1 means "1" x B = 1, which is definitely false, as 1 x B = B!
Likewise when B= 1 is assumed.
Therefore the AB = 0 cannot be applied across the board to cover all else with the same deduction.
The equal to Zero has special meaning, and should not be confused with other number equated.
In summary: AB = 0 means A= 0 or B= 0 only if "= 0".
A little accurate understanding goes a long way.... in maths, especially.
:-)
Saturday, 29 November 2008
Negative Value Equated to Exponential Expression
This is a very interesting maths question, that may trick many students.
2x = -1
What is the value for x?
I got all sort of answers.
Some gave me x = 0 (knowing that 1 = anything to the power of 0).
Some treat the expression to be 2x = -1 ==> x = -1/2.
Some used the calculator, applying "logarithm" operation and getting an "Error" message!
Those who know the answer, congratulation. You can stop reading this post.
For those interested and wanting to know what's the answer, read on...
Knowing the answer, is fine here. But knowing with understanding is better.
Now, let's put some numerical values of x into the expression.
If we choose x = +3, y = 23 = 8 ( a positive number).
If we choose x = -3, y = 2-3 = 1/8 ( a positive number).
If we choose x = 0, y = 1 (again a positive number).
Conclusion: All the x values substituted will get us positive number instead of the desired negative number.
Then how do we get a NEGATIVE number from the exponential expression?
The answer is:
WE can NEVER get a valid numerical value for x for expression in the form ax or equivalent when it is equated to a negative value.
Clear?
Do not fall into this mathematical trap. You will not look good, if you can solve it!
Have fun testing your classmate.
:-)
2x = -1
What is the value for x?
I got all sort of answers.
Some gave me x = 0 (knowing that 1 = anything to the power of 0).
Some treat the expression to be 2x = -1 ==> x = -1/2.
Some used the calculator, applying "logarithm" operation and getting an "Error" message!
Those who know the answer, congratulation. You can stop reading this post.
For those interested and wanting to know what's the answer, read on...
Knowing the answer, is fine here. But knowing with understanding is better.
Now, let's put some numerical values of x into the expression.
If we choose x = +3, y = 23 = 8 ( a positive number).
If we choose x = -3, y = 2-3 = 1/8 ( a positive number).
If we choose x = 0, y = 1 (again a positive number).
Conclusion: All the x values substituted will get us positive number instead of the desired negative number.
Then how do we get a NEGATIVE number from the exponential expression?
The answer is:
WE can NEVER get a valid numerical value for x for expression in the form ax or equivalent when it is equated to a negative value.
Clear?
Do not fall into this mathematical trap. You will not look good, if you can solve it!
Have fun testing your classmate.
:-)
Labels:
indices,
logic,
maths technique,
mistakes
Solving Index expression in Quadratic form
In maths, the solving of indices questions and its quadratic counterparts are a common practice.
Depending on how you approach the solving, you may encounter a tough journey or a smooth-flowing one.
There are, however, simple tools and concepts that can be applied, in order to have fun solving them.
Here you go....
First, let's us take an example.
Example:
(2x)2 + 3(2x) - 4 = 0
To solve this type of quadratic (index) equation, you have to take note of the common mistake in mis-interpreting the second term above.
This is the "3(2x)" term. Refer to this link for explanation on the mistake.
Next, apply the concept of using "let" to the given equation.
This is needed to simplify the mathematical expression visually. Otherwise, it may look intimidating.
To learn about the power of using "Let", click here.
With the above 2 basic steps adhered to, you are ready to move forward into a relax solving environment to handle the given equation with ease.
Simplified equation: (After letting y = 2x)
==> y2 +3y -4 = 0
Applying next, the quadratic formula method, you can see that a = 1, b= 3 and c = -4.
Solving it for y, you will get 2 values shown below. ( Click here to learn how to make use of quadractic formula to solve.)
==> y = (-3 + 5)/2 = 1 and y = (-3-5)/2 = -4
After which, solve for x.
This y is related to x by the "letting" operation you have did in the first place, that is, y = 2x.
y = 1: y = 2x ==> 2x = 1 = 20 ==> x = 0 (Answer), logical comparison.
The other answer of y = -4 will not yield any valid real answer for x here.
( Why? --- see my next post).
So, you have done the solution very easily and without hiccups if you have understood the basic concept. If you have reviewed the working here, you will notice that there is nothing complex with all the steps.
Maths can be solved through a series of mind-blowing steps. But the reverse can also be true. It is up to you to define and choose the desire path.
Do not despair initially, as you need experience to manage this selection of strategy. How to achieve this experience? Simply practice and practice.
:-) ***
Depending on how you approach the solving, you may encounter a tough journey or a smooth-flowing one.
There are, however, simple tools and concepts that can be applied, in order to have fun solving them.
Here you go....
First, let's us take an example.
Example:
(2x)2 + 3(2x) - 4 = 0
To solve this type of quadratic (index) equation, you have to take note of the common mistake in mis-interpreting the second term above.
This is the "3(2x)" term. Refer to this link for explanation on the mistake.
Next, apply the concept of using "let" to the given equation.
This is needed to simplify the mathematical expression visually. Otherwise, it may look intimidating.
To learn about the power of using "Let", click here.
With the above 2 basic steps adhered to, you are ready to move forward into a relax solving environment to handle the given equation with ease.
Simplified equation: (After letting y = 2x)
==> y2 +3y -4 = 0
Applying next, the quadratic formula method, you can see that a = 1, b= 3 and c = -4.
Solving it for y, you will get 2 values shown below. ( Click here to learn how to make use of quadractic formula to solve.)
==> y = (-3 + 5)/2 = 1 and y = (-3-5)/2 = -4
After which, solve for x.
This y is related to x by the "letting" operation you have did in the first place, that is, y = 2x.
y = 1: y = 2x ==> 2x = 1 = 20 ==> x = 0 (Answer), logical comparison.
The other answer of y = -4 will not yield any valid real answer for x here.
( Why? --- see my next post).
So, you have done the solution very easily and without hiccups if you have understood the basic concept. If you have reviewed the working here, you will notice that there is nothing complex with all the steps.
Maths can be solved through a series of mind-blowing steps. But the reverse can also be true. It is up to you to define and choose the desire path.
Do not despair initially, as you need experience to manage this selection of strategy. How to achieve this experience? Simply practice and practice.
:-) ***
Thursday, 27 November 2008
Misunderstooded Power, Exponential
In maths, there are a few basic items that need to be addressed correctly before learning carries meaning.
One of them is the understanding of the function Power or the Exponential.
When you see the expression y = 2k, what do you understand?
Is it 2 multiplied by k?
Or is it 2 multiplied k times?
This is a very common mistake or misconception by students.
2k means 2 multiplied by k times. (or 2 to the power of k).
2 to the power of 4 means 2 x 2 x 2 x 2, which written in the exponential form, becomes 24.
When this is clear, you will know that 2 x 2k is not 4k.
Which is yet another common mistake!
Then, what is this 2 x 2k?
The answer is simply 21 x 2k = 21+k.
This answer makes use of the Product Law of the index property.
To make sure you understand what I mean here, let's do another example.
5 x 23 = ?
Solution:
It is not 103 !
It is 5 x ( 2 x 2 x 2) ==> 5 x 8 = 40.
OK? Should be fine now, right?
Do not make this unnecessary mistake. 2k is NOT 2 x k.
Bid farewell to this common mistake and move on..... Cheers!
One of them is the understanding of the function Power or the Exponential.
When you see the expression y = 2k, what do you understand?
Is it 2 multiplied by k?
Or is it 2 multiplied k times?
This is a very common mistake or misconception by students.
2k means 2 multiplied by k times. (or 2 to the power of k).
2 to the power of 4 means 2 x 2 x 2 x 2, which written in the exponential form, becomes 24.
When this is clear, you will know that 2 x 2k is not 4k.
Which is yet another common mistake!
Then, what is this 2 x 2k?
The answer is simply 21 x 2k = 21+k.
This answer makes use of the Product Law of the index property.
To make sure you understand what I mean here, let's do another example.
5 x 23 = ?
Solution:
It is not 103 !
It is 5 x ( 2 x 2 x 2) ==> 5 x 8 = 40.
OK? Should be fine now, right?
Do not make this unnecessary mistake. 2k is NOT 2 x k.
Bid farewell to this common mistake and move on..... Cheers!
Labels:
mistakes
Saturday, 22 November 2008
Power of Using "Let" to Simplify Maths Solving
Anyone doing maths may encounter instances where the expressions are long and seemingly complex.
Example 1: 3(logx)2 + 4 logx + 5 = 1
Example 2: 3(1/x)2 + 4(1/x) + 5 = 1
When you jump straight into them, trying to solve them, you may encounter confusion, if inexperience with the working.
However, there is simple way to resolve this issue.
Since the mathematical expressions are complex to the eye, you can actually "simplify" them visually.
Make sure that doing any simplification, the meaning of the maths question should not change.
One technique to simplify the expression is to use "Let".
What do I mean?
Let's take the above examples to task.
Example 1: Let y = log x
The "complex" expression now becomes ==> 3 y2 + 4y + 5 = 1
Example 2: Let y = 1/x
The equation becomes also ==> 3 y2 + 4y + 5 = 1
See the usefulness of the technique here.
This technique is easy and familiar to anyone having learned simple algebra.
The above two expressions have been reduced to the familiar quadratic equations.
The only extra steps to complete the solution is the conversion back to find x.
This is so, since, solving the simplified equations give you the answer to "y", not x.
Thus, you have only to revert the "y" back to x through y = log x and y 1/x respectively.
Easy isn't it?
Maths is easy and interesting, if you want it to be.
:-)
Example 1: 3(logx)2 + 4 logx + 5 = 1
Example 2: 3(1/x)2 + 4(1/x) + 5 = 1
When you jump straight into them, trying to solve them, you may encounter confusion, if inexperience with the working.
However, there is simple way to resolve this issue.
Since the mathematical expressions are complex to the eye, you can actually "simplify" them visually.
Make sure that doing any simplification, the meaning of the maths question should not change.
One technique to simplify the expression is to use "Let".
What do I mean?
Let's take the above examples to task.
Example 1: Let y = log x
The "complex" expression now becomes ==> 3 y2 + 4y + 5 = 1
Example 2: Let y = 1/x
The equation becomes also ==> 3 y2 + 4y + 5 = 1
See the usefulness of the technique here.
This technique is easy and familiar to anyone having learned simple algebra.
The above two expressions have been reduced to the familiar quadratic equations.
The only extra steps to complete the solution is the conversion back to find x.
This is so, since, solving the simplified equations give you the answer to "y", not x.
Thus, you have only to revert the "y" back to x through y = log x and y 1/x respectively.
Easy isn't it?
Maths is easy and interesting, if you want it to be.
:-)
Labels:
Algebra,
maths technique
Tuesday, 18 November 2008
Logical Solution in Maths
Maths can be solved in many ways, as one learning it knows.
There are the conventional techniques or methods type of solving.
You follow all the rules and laws, applying them diligently to solve the problem.
It is OK, not wrong.
However, sometimes by looking at the problem, you can twist a bit and deviate to use the "logical" method to short-cut the solving.
What do I mean?
Let's look at an example.
(This method of logical thinking is applied, especailly, in solving Partial Fraction.)
5 = A(x - 1) + B (x + 2)
Find A and B.
Conventional method ==> maybe simultaneous way.
Logical mehtod.....
Let x = 1, to eliminate the unknown A, and keeping the other unknown B.
5 = A(1 -1) + B (1 + 2)
==> 5 = 0 + 3B
==> B = 5 / 3 Get it?
Now to figure out getting A.
Let x = -2, to get rid of B.
5 = A(-2-1) + B(-2 + 2)
==> 5 = (-3) A + 0
==> A = - 5/3.
Finish. Short and sharp, and easy.
This is when you apply the logical part to maths solving.
Simple trick, right? Maths is Interesting. Don't forget this.
:-)
There are the conventional techniques or methods type of solving.
You follow all the rules and laws, applying them diligently to solve the problem.
It is OK, not wrong.
However, sometimes by looking at the problem, you can twist a bit and deviate to use the "logical" method to short-cut the solving.
What do I mean?
Let's look at an example.
(This method of logical thinking is applied, especailly, in solving Partial Fraction.)
5 = A(x - 1) + B (x + 2)
Find A and B.
Conventional method ==> maybe simultaneous way.
Logical mehtod.....
Let x = 1, to eliminate the unknown A, and keeping the other unknown B.
5 = A(1 -1) + B (1 + 2)
==> 5 = 0 + 3B
==> B = 5 / 3 Get it?
Now to figure out getting A.
Let x = -2, to get rid of B.
5 = A(-2-1) + B(-2 + 2)
==> 5 = (-3) A + 0
==> A = - 5/3.
Finish. Short and sharp, and easy.
This is when you apply the logical part to maths solving.
Simple trick, right? Maths is Interesting. Don't forget this.
:-)
Labels:
Algebra,
Learning maths,
logic
Sunday, 16 November 2008
Logical Comparison in Maths
Given a maths question, most of us will attempt solving it step by step, diligently, using formula and methods we have mastered.
However, there are times when a simpler solution can be done if we are able to see the logical side to the maths problem assigned.
Let me show an example.
Question:
2x = 24, find the value of x.
Solution: (mathematically)
Taking "log" on both sides, ==> x log 2 = 4 log 2 ==> x = 4 (log 2) / (log 2) = 4
Solution: (logically)
Comparing the values of their power, we get x = 4, since their base is the same (=2).
No working is needed!
Thus, maths does not actually just train us to do things systematically, it allows us to have a bit of mental freedom. This freedom is done in terms of the small little "twists" that make use of visual comparison or logical thinking (comparison).
Interesting approach to maths learning, right?
So many ways, mathematically and non-mathematically.
But best is the stretch to our mind to develop it to see things in many angles.
.
However, there are times when a simpler solution can be done if we are able to see the logical side to the maths problem assigned.
Let me show an example.
Question:
2x = 24, find the value of x.
Solution: (mathematically)
Taking "log" on both sides, ==> x log 2 = 4 log 2 ==> x = 4 (log 2) / (log 2) = 4
Solution: (logically)
Comparing the values of their power, we get x = 4, since their base is the same (=2).
No working is needed!
Thus, maths does not actually just train us to do things systematically, it allows us to have a bit of mental freedom. This freedom is done in terms of the small little "twists" that make use of visual comparison or logical thinking (comparison).
Interesting approach to maths learning, right?
So many ways, mathematically and non-mathematically.
But best is the stretch to our mind to develop it to see things in many angles.
.
Labels:
attitude,
indices,
Learning maths,
mental maths
Friday, 14 November 2008
Tricky Square Roots

The simplified expression after the square rooting the top expression seemed easy enough.
The individual terms within the square root are handled separately to obtain what is shown.
It seems to be correct and neat. Or is it?
This is a very common mistake made by many students.
It is not correct. Do take note.
Why?
The principle of indices do not permit this type of computing.
Addition of terms has to be taken as a whole (after summation or as a complete group).
The square root is actually to the power of (1/2), which is similar to that of x2.
(x + y)(x + y) = (x + y)2
[(x + y)(x+ y)]1/2 = (x + y)
Think about it.
.
Tuesday, 21 October 2008
Algebra - Why the need?
In doing math, we are actually trying to use a systematic approach to arrive at an answer. It trains the brain to trouble-shoot problems for a consistent result.
Many a times, problems or questions can be solved through guessing and checking the answers to see if they fit the original questions. It is OK.
But if the answers are guessed wrongly, many iterations of the processes take place. It does sound correct or a better way should be better.
Algebra is therefore developed to handle this issue.
See the below simple question of finding the weight of a cheese.

Here, you can see that by guessing the weight of the cheese and checking it back with the other information, you can finally obtain the correct answer.
Another way is to use algebra. This is a systematic approach that when applied, will give you the correct answer on the first try, as opposed to the guessing method.
In the above example, you can replace the weight of the items by x, y, and z.
By solving the simultaneous equations thus formed, you can easily get the answer to the weight of the cheese.
That is the power of algebra and math. No uneducated guess, and time saving as a merit.
Practice, therefore , with algebra as the need is a necessity in our daily life.
.
Many a times, problems or questions can be solved through guessing and checking the answers to see if they fit the original questions. It is OK.
But if the answers are guessed wrongly, many iterations of the processes take place. It does sound correct or a better way should be better.
Algebra is therefore developed to handle this issue.
See the below simple question of finding the weight of a cheese.

Here, you can see that by guessing the weight of the cheese and checking it back with the other information, you can finally obtain the correct answer.
Another way is to use algebra. This is a systematic approach that when applied, will give you the correct answer on the first try, as opposed to the guessing method.
In the above example, you can replace the weight of the items by x, y, and z.
By solving the simultaneous equations thus formed, you can easily get the answer to the weight of the cheese.
That is the power of algebra and math. No uneducated guess, and time saving as a merit.
Practice, therefore , with algebra as the need is a necessity in our daily life.
.
Labels:
Algebra,
applications,
simultaneous equations
Saturday, 18 October 2008
Does Math make you clever?
Why do we need to study math?
Is this question a familiar one?
We know that we need math to do some calculations for our daily necessity. But have we to go to the extent of learning logarithm, calculus, and the more complex mathematical techniques?
Math learning also involves some form of drilling to pump in the key steps and concepts. It is also a form of structured and systematic approach to solving problems.
So does this so-called systematic approach tie us to a rigid way of doing thing?
Will math, therefore, make us a more flexible or rigid, straight-only person?
Compare this math learning to literature learning, which has more room for personal expression?
My guess, is that you will say "literature".
Yes, learning subjects, like the literature and languages , do give us the freedom of expression through writing what comes to the mind, filling in beautiful words for descriptions and the like.
Math, on the other hand, forces us to think only in a structure manner. Any deviation from the "laws" will be deemed inappropriate.
Thus, learning math makes us less clever.
WRONG!
Now let's look at learning math in another angle.
Assume you are the civil engineer having to plan the site layout for constructing a building. You are given a boundary with the area within filled with hard rocks beneath.
Another civil engineer is asked to build a similar building but now in a prairie, without any boundary constraint and the soil is marvellous.
Who has a better time?
Who need to be more experience or knowledgeable?
Who need to be better?
You have to be better.
Link this to learning math, where you are given "boundaries" to operate in. The structured approach ties you within the laws, but still requires you to come out with the answers.
Learning subjects, like the English, is equivalent to the other engineer. He has his challenges but in another form (maybe to optimise budget, appearance, etc).
So, does learning math makes you clever?
Maybe. But it will definitely not make you less clever.
Having to operate and think with more constraints requires building, in fact, more flexibilities, for you to overcome any obstacles.
This is the power of learning math, and the very reason why we need to have math in our education since young.
Interesting ironical concept, right?
(Constraints create more flexibilities).
:D
Is this question a familiar one?
We know that we need math to do some calculations for our daily necessity. But have we to go to the extent of learning logarithm, calculus, and the more complex mathematical techniques?
Math learning also involves some form of drilling to pump in the key steps and concepts. It is also a form of structured and systematic approach to solving problems.
So does this so-called systematic approach tie us to a rigid way of doing thing?
Will math, therefore, make us a more flexible or rigid, straight-only person?
Compare this math learning to literature learning, which has more room for personal expression?
My guess, is that you will say "literature".
Yes, learning subjects, like the literature and languages , do give us the freedom of expression through writing what comes to the mind, filling in beautiful words for descriptions and the like.
Math, on the other hand, forces us to think only in a structure manner. Any deviation from the "laws" will be deemed inappropriate.
Thus, learning math makes us less clever.
WRONG!
Now let's look at learning math in another angle.
Assume you are the civil engineer having to plan the site layout for constructing a building. You are given a boundary with the area within filled with hard rocks beneath.
Another civil engineer is asked to build a similar building but now in a prairie, without any boundary constraint and the soil is marvellous.
Who has a better time?
Who need to be more experience or knowledgeable?
Who need to be better?
You have to be better.
Link this to learning math, where you are given "boundaries" to operate in. The structured approach ties you within the laws, but still requires you to come out with the answers.
Learning subjects, like the English, is equivalent to the other engineer. He has his challenges but in another form (maybe to optimise budget, appearance, etc).
So, does learning math makes you clever?
Maybe. But it will definitely not make you less clever.
Having to operate and think with more constraints requires building, in fact, more flexibilities, for you to overcome any obstacles.
This is the power of learning math, and the very reason why we need to have math in our education since young.
Interesting ironical concept, right?
(Constraints create more flexibilities).
:D
Labels:
attitude,
Learning maths
Tuesday, 14 October 2008
Scalar Multiplication in Determinant and Matrices
The study of determinants and matrices can be confusing at time. They look almost the same, and are closely related. As such, some mathematical operations on them are similar.
But, there are differ somewhat and have to be taken care of.
Below is one such mistake that is often made by learning math students.

The upper row involves matrices. The scalar multiplication of it by "a" affects ALL the elements within the matrix.
For the lower row, the scalar "a" multiplication affects only one column (or one row) of the determinant.
Just note this different and commit it to memory. This is good for you and can save you a lot of further troubles with matrix and determinant.
So, just simply identifying the differences between matrices and determinant, in term of their operations, you will be enjoying them for a long time.
With less mistake made, you will be more gear towards doing a better job out of maths. This is human nature.
Cheers! and Happy mathematics!
:D
But, there are differ somewhat and have to be taken care of.
Below is one such mistake that is often made by learning math students.

The upper row involves matrices. The scalar multiplication of it by "a" affects ALL the elements within the matrix.
For the lower row, the scalar "a" multiplication affects only one column (or one row) of the determinant.
Just note this different and commit it to memory. This is good for you and can save you a lot of further troubles with matrix and determinant.
So, just simply identifying the differences between matrices and determinant, in term of their operations, you will be enjoying them for a long time.
With less mistake made, you will be more gear towards doing a better job out of maths. This is human nature.
Cheers! and Happy mathematics!
:D
Labels:
determinant,
matrices
Tuesday, 7 October 2008
Lines of Wisdom
In an earlier post, the enjoyment of knowing maths was demonstrated in its ability to form pictures.
Here is another example of playing with the trigonometry to create mathematical art.

In this piece of art, 4 graphs of various mathematical expressions were overlapped to form the result.
I name this piece of art the "Lines of Wisdom".
In the graphs, maths functions like the sine and sinh operation were used together with trigonometrical multiplication.
:D
Here is another example of playing with the trigonometry to create mathematical art.

In this piece of art, 4 graphs of various mathematical expressions were overlapped to form the result.
I name this piece of art the "Lines of Wisdom".
In the graphs, maths functions like the sine and sinh operation were used together with trigonometrical multiplication.
:D
Labels:
Fun in maths,
graphical art,
Trigonometry
Sunday, 5 October 2008
Creating A Maths Picture
Maths can be used in many ways.
It is normally used to solve daily calculations related to work, life, etc.
It can be used to model a system to understand its performance and behaviour.
However, on the fun side, it can be used to create a picture using graph as a means.
Here in this post, a picture formed through merging trigonometry with modulation technique is shown.

What do you think this picture is about?
While creating this maths picture, a kid so happened to have a glimpse of it, and commented that it looked like the front view of an aeroplane.
For me, it seems to be the captured voice of Optimus Prime, the Transformer Autobot leader.
With maths, if you understand the underlying principles of various elementary topics, you can freely come up with any mathematical figures that you wish.
Here, I have simply used the special sinc function modulated (multiplied) by a high frequency trigonometric sine function to get this mixed result.
Using graph is one way to form picture, like the one created here.
It is fun seeing your imagination materialise through using maths and graphs as the tools.
Try it for yourself. You will enjoy maths and its fun picture creation.
:D
It is normally used to solve daily calculations related to work, life, etc.
It can be used to model a system to understand its performance and behaviour.
However, on the fun side, it can be used to create a picture using graph as a means.
Here in this post, a picture formed through merging trigonometry with modulation technique is shown.

What do you think this picture is about?
While creating this maths picture, a kid so happened to have a glimpse of it, and commented that it looked like the front view of an aeroplane.
For me, it seems to be the captured voice of Optimus Prime, the Transformer Autobot leader.
With maths, if you understand the underlying principles of various elementary topics, you can freely come up with any mathematical figures that you wish.
Here, I have simply used the special sinc function modulated (multiplied) by a high frequency trigonometric sine function to get this mixed result.
Using graph is one way to form picture, like the one created here.
It is fun seeing your imagination materialise through using maths and graphs as the tools.
Try it for yourself. You will enjoy maths and its fun picture creation.
:D
Labels:
Fun in maths,
graph,
graphical art,
Trigonometry
Monday, 29 September 2008
Is Maths Fearful?
Everyone is frighten of something. Everyone has "likes" and "don't likes".
We are human. We have emotion, temperament and preferences.
Knowing that, you are in the correct path to math learning.
What is so fearful about maths?
Or rather why are you frighten of a particular thing?
We are frighten of certain things because, we are simply, not in control of that thing.
We do not know when it will come, or when will it happen.
When it occurs, we are not able to handle it.
So you see the problem now?
Now that you see the problem or problems, the next step is to resolve them. Logical, right?
Let's for here, focus on this maths issue.
Maths, when you really look at it, does not have any fantastic things within it.
What it has is the normal numbers, symbols, equations, formula, etc. Nothing great.
What is fearful is the relationship between all the elements.
Handling relationship is always a tricky problem, similarly to human matters.
Therefore, identify which part of this relation you have trouble with.
Is it that you forgot the meaning of the symbol, thus resulting in non-linking of the equation?
Is it technique of solving that poses an obstacle? The relationship of method to expression?
Learn to solve this maths hiccups and untangle the knots. Rid yourself of the "fear", that is apparently when you are not in control.
Control your learning. Pay attention to the math teacher. Do your assignment properly. Do not copy answers. Seek for understanding.
These are a few suggestions that I can present here for your reference, and hopefully, twist your fear for math to liking math.
Maths is not that difficult. It is just a subject to test our mind only.
:-)
We are human. We have emotion, temperament and preferences.
Knowing that, you are in the correct path to math learning.
What is so fearful about maths?
Or rather why are you frighten of a particular thing?
We are frighten of certain things because, we are simply, not in control of that thing.
We do not know when it will come, or when will it happen.
When it occurs, we are not able to handle it.
So you see the problem now?
Now that you see the problem or problems, the next step is to resolve them. Logical, right?
Let's for here, focus on this maths issue.
Maths, when you really look at it, does not have any fantastic things within it.
What it has is the normal numbers, symbols, equations, formula, etc. Nothing great.
What is fearful is the relationship between all the elements.
Handling relationship is always a tricky problem, similarly to human matters.
Therefore, identify which part of this relation you have trouble with.
Is it that you forgot the meaning of the symbol, thus resulting in non-linking of the equation?
Is it technique of solving that poses an obstacle? The relationship of method to expression?
Learn to solve this maths hiccups and untangle the knots. Rid yourself of the "fear", that is apparently when you are not in control.
Control your learning. Pay attention to the math teacher. Do your assignment properly. Do not copy answers. Seek for understanding.
These are a few suggestions that I can present here for your reference, and hopefully, twist your fear for math to liking math.
Maths is not that difficult. It is just a subject to test our mind only.
:-)
Labels:
Learning maths
Thursday, 25 September 2008
How To Transpose A Matrix
Transposing a matrix is a term for a process that "swap" the row of a matrix with its column.
All the elements within the matrix remain except for their placement.
NOTE: Matrix transpose is important and a key step in getting the Inverse matrix which is required in the solving of simultaneous equations.
The procedure to transpose is simple, but saying that, caution has to be taken of which direction to "rotate". Look carefully at the coloured elements to see the direction (below diagram).

Here you see that the symbol to represent "Transpose" s the "T" besides the original matrix. The elements remain intact and not shifted yet.
Only upon transposing, the "T" disappeared.
Now, see how the transposed elements are done.
The first row is changed to the first column, with the element "a" being the pivot point.
Common mistake:
The pivot point (element) is taken wrongly. Normally element "c" is the target which is incorrect!
Stay focus when doing this transpose. You will then rid yourself of less trouble.
Cheers! Remember, maths is interesting! (If you are doing the correct thing.)
.
All the elements within the matrix remain except for their placement.
NOTE: Matrix transpose is important and a key step in getting the Inverse matrix which is required in the solving of simultaneous equations.
The procedure to transpose is simple, but saying that, caution has to be taken of which direction to "rotate". Look carefully at the coloured elements to see the direction (below diagram).

Here you see that the symbol to represent "Transpose" s the "T" besides the original matrix. The elements remain intact and not shifted yet.
Only upon transposing, the "T" disappeared.
Now, see how the transposed elements are done.
The first row is changed to the first column, with the element "a" being the pivot point.
Common mistake:
The pivot point (element) is taken wrongly. Normally element "c" is the target which is incorrect!
Stay focus when doing this transpose. You will then rid yourself of less trouble.
Cheers! Remember, maths is interesting! (If you are doing the correct thing.)
.
Labels:
matrices
Wednesday, 24 September 2008
How to do the 3 x 3 order determinant using Rule of Sarrus
It is very often that we come across the word determinant in matrices. Yes, they are related.
Matrix consists a set of numbers. That's it.
Determinant is a numerical value obtained throught the numbers within the matrix.
For a 3 x 3 matrix, how then do we extract the determinant?
One of the easiest method to obtain this number is throught the use of Rule of Sarrus.
Below I show the steps.

Determinant A = [(aei) + (bfg) + (cdh) ] - [ (gec) + (hfa) + (idb) ].
=====================================================>>>
The important step lies with getting the first left 2 columns out to the right of the determinant.
After which, we do a downwards grouping and addition.
This is followed by upwards grouping with addition again.
Note, the last step is to SUBTRACT the two groups obtained above.
(By grouping, I mean to MULTIPLY the individual elements).
Common mistakes:
1) The grouping is done by "adding" instead of multiplying the elements.
2) The slanted operations (the 3 element-multiplication) are done by "adding" instead of multiplying the 3 elements.
3) The two big groups are "added" instead of subtracted".
Just bear in mind the 3 common mistakes above and you are on the way to a happy matrix student...
Cheers!
Matrix consists a set of numbers. That's it.
Determinant is a numerical value obtained throught the numbers within the matrix.
For a 3 x 3 matrix, how then do we extract the determinant?
One of the easiest method to obtain this number is throught the use of Rule of Sarrus.
Below I show the steps.

Determinant A = [(aei) + (bfg) + (cdh) ] - [ (gec) + (hfa) + (idb) ].
=====================================================>>>
The important step lies with getting the first left 2 columns out to the right of the determinant.
After which, we do a downwards grouping and addition.
This is followed by upwards grouping with addition again.
Note, the last step is to SUBTRACT the two groups obtained above.
(By grouping, I mean to MULTIPLY the individual elements).
Common mistakes:
1) The grouping is done by "adding" instead of multiplying the elements.
2) The slanted operations (the 3 element-multiplication) are done by "adding" instead of multiplying the 3 elements.
3) The two big groups are "added" instead of subtracted".
Just bear in mind the 3 common mistakes above and you are on the way to a happy matrix student...
Cheers!
Labels:
matrices
Monday, 22 September 2008
Curious Maths Terms
Have some fun with the terms used in maths...
1) Doing multiplication without tables ===> Doing the maths problems on the floor
2) Using integration ===> Discussing with classmates and copying relevant answers
3) Using differentiation ===> Sorting out what can be done and what can't
4) Finding partial fractions ===> allowed to complete the computation partially
5) Calculating standard deviation ===> finding out how many more marks to hit standard pass grade
Caution:
Do not take this too serious, otherwise ....... you will really have to check your standard deviation.
.
1) Doing multiplication without tables ===> Doing the maths problems on the floor
2) Using integration ===> Discussing with classmates and copying relevant answers
3) Using differentiation ===> Sorting out what can be done and what can't
4) Finding partial fractions ===> allowed to complete the computation partially
5) Calculating standard deviation ===> finding out how many more marks to hit standard pass grade
Caution:
Do not take this too serious, otherwise ....... you will really have to check your standard deviation.
.
Labels:
Fun in maths
Wednesday, 17 September 2008
Multiplication of Matrices
As do normal number multiplication, matrices themselves, also have their set of multiplication.
They are however done in another interesting way.
This is so since a matrix consists of a set of numbers within it.
Therefore multiplying matrices are not so straight forward as normal numbers.
But do rest assure that there is nothing new, it is still simple multiplication ( and addition / subtraction).
Maths is simple and interesting, remember? Read on for the steps and caution points.
Below I show multiplication using 2 matrices of the 2 x 2 order.
Do note that I have presented the steps first, leaving out the technical computation later on in this post (below the diagram).
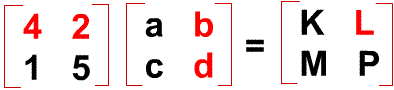
See below for the steps:
.
They are however done in another interesting way.
This is so since a matrix consists of a set of numbers within it.
Therefore multiplying matrices are not so straight forward as normal numbers.
But do rest assure that there is nothing new, it is still simple multiplication ( and addition / subtraction).
Maths is simple and interesting, remember? Read on for the steps and caution points.
Below I show multiplication using 2 matrices of the 2 x 2 order.
Do note that I have presented the steps first, leaving out the technical computation later on in this post (below the diagram).
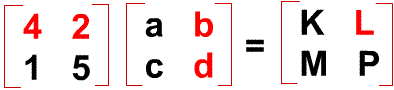
See below for the steps:
- element "K" is obtained from the first row of left matrix and the first column of the next matrix,
- element "L" is obtained using first row of left matrix and SECOND column f next matrix.
- element "M" is obtained using SECOND row of left matrix and first column of next matrix.
- element "P" is using second row and column of the respective matrices.
These sequence is of utmost importance. Why?
By not following the sequence to obtain the final elements, the numbers will be simply messed up! This is a very common mistake among students of matrices.
It is mental discipline to systematically derive the elements in the appropriate positions.
Next, let us go into getting the actual number for the final elements. Here we go...
Elements "K" = (4 x a) + (2 x c)
Element "L" = (4 x b) + (2 x d)
Element "M" = (1 x a) + (5 x c)
Element "N" = (1 x b) + (5 x d) ===> There is it, you have gotten all the elements!
There is nothing difficult, right? Matrix study is one of the simplest topics in maths.
Have fun!
.
Labels:
matrices
Thursday, 11 September 2008
Math Challenge (10)
It is time for us to play some math game.
You do not need a university degree to handle this game.
Everyone can play. It is meant to exercise your brain, nothing taxing.
What is this game about?
Challenge
There is a series of numbers that you have to add mathematical operators (+, -, / , x or brackets) to. The addition of these operators has to satisfy the end result though.
Example:
2 2 2 2 = 0 => Solution is 2 + 2 - 2 - 2 = 0
2 2 2 2 = 1
2 2 2 2 = 2
2 2 2 2 = 3
2 2 2 2 = 4
2 2 2 2 = 5
2 2 2 2 = 6
2 2 2 2 = 7
2 2 2 2 = 8
2 2 2 2 = 9
Nothing difficult, right? It is just to get your brain moving, otherwise it will go rusty.
Enjoy yourself.
You may also alter the list to include other numbers.
4 4 5 5 = 1
4 4 5 5 = 2
4 4 5 5 = 3
and so on .......
:-)
You do not need a university degree to handle this game.
Everyone can play. It is meant to exercise your brain, nothing taxing.
What is this game about?
Challenge
There is a series of numbers that you have to add mathematical operators (+, -, / , x or brackets) to. The addition of these operators has to satisfy the end result though.
Example:
2 2 2 2 = 0 => Solution is 2 + 2 - 2 - 2 = 0
2 2 2 2 = 1
2 2 2 2 = 2
2 2 2 2 = 3
2 2 2 2 = 4
2 2 2 2 = 5
2 2 2 2 = 6
2 2 2 2 = 7
2 2 2 2 = 8
2 2 2 2 = 9
Nothing difficult, right? It is just to get your brain moving, otherwise it will go rusty.
Enjoy yourself.
You may also alter the list to include other numbers.
4 4 5 5 = 1
4 4 5 5 = 2
4 4 5 5 = 3
and so on .......
:-)
Labels:
Maths Thinker
Sunday, 7 September 2008
Matrices | What is Minor?
Before you read this, say "maths is interesting!". Mental trick....
Now you may start.
In matrices, there is an important basic term residing in it.
It is the term called "minor" and is obtained through the determinant of the matrix.
For 2nd order matrix (or determinant), there will be 4 minors since there are 4 elements within the determinant.
For 3rd order form, there will inevitably, be 9 minors.
To have an idea what "order of matrix" is about, go to this link here.
How to compute this minor?
See below...
The method is simple, right?
It involves the correct cancellation of the appropriate row and column.
The leftover elements will be used to determine the value.
To enhance understanding, let's do another example.Find the minor of element 2.
The leftover is the elements
4 6
7 9
The determinant value of the leftover is then (4)(9) - (7)(6) = 36 - 42 = -6.
This is the minor for element "2".
Common mistake made:
The minor is always taken as the actual element in question.
Example of mistakes:
To find the minor of element "2" in the above determinant
==> Wrong answer = "2", the original element used to get the leftover after cancellation.
To find the minor of element "1" in the above determinant
==> Wrong answer = "1", the original element used to get the leftover after cancellation.
NOTE:
Minor and Co-factor are closely related. They are needed to compute Adjoint and Inverse matrix.
You have to master these concepts to be able to handle matrices.
Tough, right? If your answer is YES, you are wrong!
Look and review the above methods again, and you will be sure that they are simply +, _, x only.
Isn't this what you have been learning since lower elementary?
:-)
Now you may start.
In matrices, there is an important basic term residing in it.
It is the term called "minor" and is obtained through the determinant of the matrix.
For 2nd order matrix (or determinant), there will be 4 minors since there are 4 elements within the determinant.
For 3rd order form, there will inevitably, be 9 minors.
To have an idea what "order of matrix" is about, go to this link here.
How to compute this minor?
See below...
The method is simple, right?
It involves the correct cancellation of the appropriate row and column.
The leftover elements will be used to determine the value.
To enhance understanding, let's do another example.Find the minor of element 2.
The leftover is the elements
4 6
7 9
The determinant value of the leftover is then (4)(9) - (7)(6) = 36 - 42 = -6.
This is the minor for element "2".
Common mistake made:
The minor is always taken as the actual element in question.
Example of mistakes:
To find the minor of element "2" in the above determinant
==> Wrong answer = "2", the original element used to get the leftover after cancellation.
To find the minor of element "1" in the above determinant
==> Wrong answer = "1", the original element used to get the leftover after cancellation.
NOTE:
Minor and Co-factor are closely related. They are needed to compute Adjoint and Inverse matrix.
You have to master these concepts to be able to handle matrices.
Tough, right? If your answer is YES, you are wrong!
Look and review the above methods again, and you will be sure that they are simply +, _, x only.
Isn't this what you have been learning since lower elementary?
:-)
Labels:
matrices
How To Get Determinant Value
In the study of matrices, you will come across the computation of determinant and their values.
These determinants come in various order.
There are the 2nd order, 3rd order, and so on.
What is this order?
Order is the number of rows and column within the determinant.
Thus, 2nd order determinant has 2 rows and 2 columns.
3rd order has 3 rows and 3 columns.
To calculate the values of these determinants, see below for the methods.

The 2nd order is shown in the first upper line.
Following that is the 3rd order computation, using the special Rule of Sarrus (the simpler form of 3rd order calculation).
This value computed comes in useful to determine other values.
One of the examples is the solution of simultaneous equations and their unknowns.
The technique presented here is thus, basic knowledge in matrices learning.
These determinants come in various order.
There are the 2nd order, 3rd order, and so on.
What is this order?
Order is the number of rows and column within the determinant.
Thus, 2nd order determinant has 2 rows and 2 columns.
3rd order has 3 rows and 3 columns.
To calculate the values of these determinants, see below for the methods.

The 2nd order is shown in the first upper line.
Following that is the 3rd order computation, using the special Rule of Sarrus (the simpler form of 3rd order calculation).
This value computed comes in useful to determine other values.
One of the examples is the solution of simultaneous equations and their unknowns.
The technique presented here is thus, basic knowledge in matrices learning.
Labels:
matrices
Saturday, 6 September 2008
Adjoint and Inverse Matrix } Their relationship
There is a common misunderstanding among math learners over the common term in matrices.
The two terms are the Adjoint and Inverse matrix.
The operation to get them is somewhat always confused and "mixed up".
Here to clear and simplify their differences:
- Adjoint matrix
It is obtained through the co-factors of each elements within the matrix. After which the matrix is transposed. It stops there.
- Inverse matrix
The adjoint matrix forms part of this inverse matrix!
Inverse matrix needs a further computation of the determinant also.
The final outcome is the adjoint matrix divided by this determinant value.
Therefore in summary, inverse matrix is formed out of the adjoint matrix.
They are husband and wife, with the kids, the minor and co-factors in them.
.
The two terms are the Adjoint and Inverse matrix.
The operation to get them is somewhat always confused and "mixed up".
Here to clear and simplify their differences:
- Adjoint matrix
It is obtained through the co-factors of each elements within the matrix. After which the matrix is transposed. It stops there.
- Inverse matrix
The adjoint matrix forms part of this inverse matrix!
Inverse matrix needs a further computation of the determinant also.
The final outcome is the adjoint matrix divided by this determinant value.
Therefore in summary, inverse matrix is formed out of the adjoint matrix.
They are husband and wife, with the kids, the minor and co-factors in them.
.
Labels:
matrices
Sunday, 31 August 2008
Inverse Matrix | What is it used for?
One of the applications of inverse matrix is in solving simultaneous equations.
If you are good with algebra, you will discover that this inverse matrix way of handling the solution of simultaneous equations is similar, except that they are done as a group, collectively.
The answers to the unknown variables are obtained at one go with this Inverse matrix method.
However, what do you need to know in order to use this Inverse matrix solving?
You have to understand:
1) Convertion of simultaneous equations into a set of matrices
2) Determinant and technique to get its numerical value
3) Minor of the individual elements within the matrix
4) Co-factor of this determinant formed with this set of matrices
5) Transpose of matrix
6) Adjoint matrix obtained with the co-factors and transposed matrix
7) Formula to relate determinant with the adjoint matrix ==> Inverse matrix
8) Matrices multiplication
The list looks amazingly long for matrix novice, but, DO NOT FEAR!
Why?
Matrices consist of numbers only, and simple mathematical operations, nothing abstract.
(The details are not presented here for fear that you will leave this site.)
Slowly research into the above terms and see for yourself that they are "friends" and not "foes".
Happy start to matrices and its application.
.
If you are good with algebra, you will discover that this inverse matrix way of handling the solution of simultaneous equations is similar, except that they are done as a group, collectively.
The answers to the unknown variables are obtained at one go with this Inverse matrix method.
However, what do you need to know in order to use this Inverse matrix solving?
You have to understand:
1) Convertion of simultaneous equations into a set of matrices
2) Determinant and technique to get its numerical value
3) Minor of the individual elements within the matrix
4) Co-factor of this determinant formed with this set of matrices
5) Transpose of matrix
6) Adjoint matrix obtained with the co-factors and transposed matrix
7) Formula to relate determinant with the adjoint matrix ==> Inverse matrix
8) Matrices multiplication
The list looks amazingly long for matrix novice, but, DO NOT FEAR!
Why?
Matrices consist of numbers only, and simple mathematical operations, nothing abstract.
(The details are not presented here for fear that you will leave this site.)
Slowly research into the above terms and see for yourself that they are "friends" and not "foes".
Happy start to matrices and its application.
.
Labels:
matrices
Monday, 25 August 2008
Graphical Art (Jelly Fish)
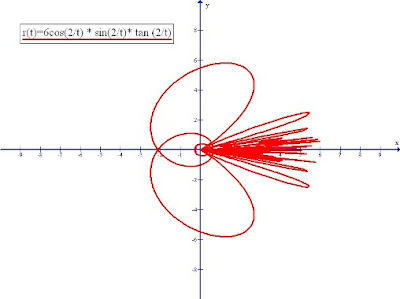 What does the above graph looks like?
What does the above graph looks like?A jelly fish drawn out of trigonometrical expressions. Wondering what is maths about...
Yes, on the interesting part, maths is lively, as seen above.
Animals come alive with maths.....
.
Labels:
graphical art
Graphical Art (Volcano)
The piece of graphical art above reflects the beauty of mathematical functions when plotted.
It not only shows the trend of the equation , it can be used to draw figures.
The above diagram is drawn using trigonometrical functions, and to me, it looks like a volcano.
What do you think?
Maths is interesting, in this aspect, right?
.
Labels:
graphical art
Saturday, 23 August 2008
Differences between Determinants and Matrices
Determinants and matrices, they look alike. Their similarities caught many unaware and results in "excitements" and much interests.
Both contain numbers within. But ......
- determinants are bounded by two straights lines whereas matrices are by square braces
- determinant resulted in a single numerical value, whereas matrices are sets of numbers grouped within the braces
- determinant can be extracted from matrix, but not the other way round
- there are inverse matrix but not inverse determinant
- a scalar multiplier affects only a single row or single column of a determinant, but affects all the numbers within a matrix
The differences are aplenty. But those listed above are the least any maths students or person should know.
Why create such topics to excite maths learners?
Answer: So that maths will be made interesting and challenging (... the informal reply)
With open mindedness, maths is a very fantastic subject to learn and train for. It carries many hard works and beautiful thinking. Thoughts that are simple yet abstract at times.
Any more fun? ..... You are the answer!
.
Both contain numbers within. But ......
- determinants are bounded by two straights lines whereas matrices are by square braces
- determinant resulted in a single numerical value, whereas matrices are sets of numbers grouped within the braces
- determinant can be extracted from matrix, but not the other way round
- there are inverse matrix but not inverse determinant
- a scalar multiplier affects only a single row or single column of a determinant, but affects all the numbers within a matrix
The differences are aplenty. But those listed above are the least any maths students or person should know.
Why create such topics to excite maths learners?
Answer: So that maths will be made interesting and challenging (... the informal reply)
With open mindedness, maths is a very fantastic subject to learn and train for. It carries many hard works and beautiful thinking. Thoughts that are simple yet abstract at times.
Any more fun? ..... You are the answer!
.
Labels:
matrices
Wednesday, 20 August 2008
Cramer and Sarrus | How are they related to maths
Cramer and Sarrus?
Who are they?
In which area of maths are they involved?
For those of you who is doing matrices, you will be familiar with their rules, I suppose.
They are famous for creating techniques used in the solution of simultaneous equations.
How so?
Cramer's Rule is a method of solving unknowns in simultaneous equations using division of various determinants.
Rule of Sarrus is a simple way of determining the numerical value of 3rd order determinant.
The two rules, therefore, complement each other to form an easy way to solve simultaneous equations.
However do note that students of these topics use to mix up the 2 rules.
When question states the use of Cramer's and Sarrus rule, they tend to get confuse. THe common notion is that Rule of Sarrus is another method to solve simultaneous equations which is not so.
It is only a technique to evaluate the determinant and get its value. It cannot solve the unknowns in the set of equations.
This is a good problem to get confuse. Why?
Getting confuse means a thinking brain and learning starts to take place. When there is no confusion, there can be two happenings.
- blank or "completely do not understand"
- "completely understood without questions"
Which is which does not matter. What is important is not to disappoint Cramer and Sarrus!
Work hard folks!
Cheers!
:-)
Who are they?
In which area of maths are they involved?
For those of you who is doing matrices, you will be familiar with their rules, I suppose.
They are famous for creating techniques used in the solution of simultaneous equations.
How so?
Cramer's Rule is a method of solving unknowns in simultaneous equations using division of various determinants.
Rule of Sarrus is a simple way of determining the numerical value of 3rd order determinant.
The two rules, therefore, complement each other to form an easy way to solve simultaneous equations.
However do note that students of these topics use to mix up the 2 rules.
When question states the use of Cramer's and Sarrus rule, they tend to get confuse. THe common notion is that Rule of Sarrus is another method to solve simultaneous equations which is not so.
It is only a technique to evaluate the determinant and get its value. It cannot solve the unknowns in the set of equations.
This is a good problem to get confuse. Why?
Getting confuse means a thinking brain and learning starts to take place. When there is no confusion, there can be two happenings.
- blank or "completely do not understand"
- "completely understood without questions"
Which is which does not matter. What is important is not to disappoint Cramer and Sarrus!
Work hard folks!
Cheers!
:-)
Labels:
determinant,
matrices
Tuesday, 19 August 2008
A Good Quadratic Solver
I chanced upon a good math solving tools that every math learners will love.
Even though you may not use it to solve math problems, you can take this Quadratic solver as a guide to check your answers.
It is a user-friendly tool that can give you the answer easily. Try it!
This is one of the easily available math tools that make maths learning exciting and and interesting. See for yourself.
Quadratic Solver
This solver is provided by Algebra.Com:
.
Even though you may not use it to solve math problems, you can take this Quadratic solver as a guide to check your answers.
It is a user-friendly tool that can give you the answer easily. Try it!
This is one of the easily available math tools that make maths learning exciting and and interesting. See for yourself.
Quadratic Solver
This solver is provided by Algebra.Com:
.
Labels:
Algebra
Log X Is Just A Number
I happened to come across an interesting mistake made by a maths student.
The mistake inter-mixed the principles of algebra with logarithm.
The maths question is to solve the value of x given the expression:
2+ log (5x - 1) = log 3x
The expression, after transferring the "log (5x -1)" to the right side of the "=", became
2 = log 3x - log (-5x + 1) !
Spotted the mistake done ?
Why was the "log (-5x + 1)" in that form?
The correct expression should be 2 = log 3x - log (5x - 1).
What actually went inside the student's mind was confusion between algebra and logarithm. He did not understand the concept of "logging" the (5x -1).
Log X is always a number!
Similarly log (5x - 1) is also a number.
Therefore log (5x - 1) moves as a number, same as in moving algebraic term.
If we have 2 + (x-a) = y, re-arranging the expression, gives us 2 = y - ( x-a).
The term "x-a" is taken as a whole, with change in the sign of (x -a) and not including that of the individual internal "a" and "x". This is basic algebra.
Moving log (5x - 1) is the same. Being a number, it operates equivalent to the algebraic manipulation.
The log (5x -1) is thus taken as a whole and sign change affects only the term as a whole. It does not affect the individual internal "5x" and "-1"!
Part of learning maths is following rules and principles.
The mistake made by the student was a reflection of correct algebraic change, but in the wrong sense. "Log" had converted the term into a number, and that was the mistake not captured.
Being careful with every steps taken in solving maths questions is a discipline one can treasure. This is one of the interesting part of doing maths!
<*_*>
.
The mistake inter-mixed the principles of algebra with logarithm.
The maths question is to solve the value of x given the expression:
2+ log (5x - 1) = log 3x
The expression, after transferring the "log (5x -1)" to the right side of the "=", became
2 = log 3x - log (-5x + 1) !
Spotted the mistake done ?
Why was the "log (-5x + 1)" in that form?
The correct expression should be 2 = log 3x - log (5x - 1).
What actually went inside the student's mind was confusion between algebra and logarithm. He did not understand the concept of "logging" the (5x -1).
Log X is always a number!
Similarly log (5x - 1) is also a number.
Therefore log (5x - 1) moves as a number, same as in moving algebraic term.
If we have 2 + (x-a) = y, re-arranging the expression, gives us 2 = y - ( x-a).
The term "x-a" is taken as a whole, with change in the sign of (x -a) and not including that of the individual internal "a" and "x". This is basic algebra.
Moving log (5x - 1) is the same. Being a number, it operates equivalent to the algebraic manipulation.
The log (5x -1) is thus taken as a whole and sign change affects only the term as a whole. It does not affect the individual internal "5x" and "-1"!
Part of learning maths is following rules and principles.
The mistake made by the student was a reflection of correct algebraic change, but in the wrong sense. "Log" had converted the term into a number, and that was the mistake not captured.
Being careful with every steps taken in solving maths questions is a discipline one can treasure. This is one of the interesting part of doing maths!
<*_*>
.
Labels:
Logarithm
"+" Its Many Interpretations
Maths consists of many symbols. The four basic maathematical operators are the "+", "-", "/" and "x".
We use them easily in many maths expressions. In normal usage, they are maths operator. But there are some instances where their meaning deviates and is important that the maths learners are aware of.
This deviation to the normal meaning happens to allow maatching to the application.
Let's take a simple example of the "+" operation.
Case 1:
H + H + O = H2O
This is the addition of chemical elements with a different results from normal maaths.
The interpretation differs to suit the chemical equation. It is valid. But not for true maaths!
Case 2:
A + A = A
Why is it not A + A = 2A?
This is an instance of the Boolean Algebra. In boolean operation, there is no "2", being in base 2.
In boolean or digital operation, the "A" can mean a "High" logic or "1".
Therefore, a "High" added to "High" will still give a "High" logic (in the electrical sense).
Thus A + A = A ==> Still a valid add (+) operation in this digital sense.
Case 3:
a++
In this case, the operation is actually an abbreviation of a programming language.
What it really does is to replace the result of a mathematical operation of a + 1 back to itself.
A location called "a" is provided (in hardware) and the results of the operation "a + 1" is placed back to the "a" location. This is again a valid "+" process with a different meaning to the normal maths operation.
The 3 cases highlighted serves to let maths learners know that the symbol "+", though looks simple, is also subjected to many interpretations. Thus everyone needs to be aware of its matching to the specific applications.
:)
We use them easily in many maths expressions. In normal usage, they are maths operator. But there are some instances where their meaning deviates and is important that the maths learners are aware of.
This deviation to the normal meaning happens to allow maatching to the application.
Let's take a simple example of the "+" operation.
Case 1:
H + H + O = H2O
This is the addition of chemical elements with a different results from normal maaths.
The interpretation differs to suit the chemical equation. It is valid. But not for true maaths!
Case 2:
A + A = A
Why is it not A + A = 2A?
This is an instance of the Boolean Algebra. In boolean operation, there is no "2", being in base 2.
In boolean or digital operation, the "A" can mean a "High" logic or "1".
Therefore, a "High" added to "High" will still give a "High" logic (in the electrical sense).
Thus A + A = A ==> Still a valid add (+) operation in this digital sense.
Case 3:
a++
In this case, the operation is actually an abbreviation of a programming language.
What it really does is to replace the result of a mathematical operation of a + 1 back to itself.
A location called "a" is provided (in hardware) and the results of the operation "a + 1" is placed back to the "a" location. This is again a valid "+" process with a different meaning to the normal maths operation.
The 3 cases highlighted serves to let maths learners know that the symbol "+", though looks simple, is also subjected to many interpretations. Thus everyone needs to be aware of its matching to the specific applications.
:)
Labels:
Algebra
Mental Alertness In Maths Calculation
We are human after-all. Why do I say that?
Did you make simple maths error especially after a certain period of performing maths calculations?
Our mind has to have the strength and stamina to stay active and alert to have 0% error.
This is not a maths problem. Rather it is a psychological problem.
How then are we to minimise, if not eliminate, these simple maths errors that we hate to make?
Below I list a simple trick that I often used and advise maths learners.
- Before starting to do any maths assignment, or test, or examination, scan through the whole paper to scout out the simple and difficult questions.
- Start off with the complex questions or those that you are not that confident with. You need the attention to "attack" those questions while your brain is still alert. (Note the time factor too, otherwise, you may consume too much time for them leaving little time for the simple ones!)
- After completing the complex questions, you will be more relax mentally to solve the other questions. And given the simplicity, less error will be made since you have scanned through the paper initially and has better confidence in dealing with them.
This is a proposal that balance mental alertness with solving math questions.
Maths solving can be taxing, but with proper strategy, you can lessen the anxiety and, in fact, after more practice, like and enjoy maths.
:-)
Did you make simple maths error especially after a certain period of performing maths calculations?
Our mind has to have the strength and stamina to stay active and alert to have 0% error.
This is not a maths problem. Rather it is a psychological problem.
How then are we to minimise, if not eliminate, these simple maths errors that we hate to make?
Below I list a simple trick that I often used and advise maths learners.
- Before starting to do any maths assignment, or test, or examination, scan through the whole paper to scout out the simple and difficult questions.
- Start off with the complex questions or those that you are not that confident with. You need the attention to "attack" those questions while your brain is still alert. (Note the time factor too, otherwise, you may consume too much time for them leaving little time for the simple ones!)
- After completing the complex questions, you will be more relax mentally to solve the other questions. And given the simplicity, less error will be made since you have scanned through the paper initially and has better confidence in dealing with them.
This is a proposal that balance mental alertness with solving math questions.
Maths solving can be taxing, but with proper strategy, you can lessen the anxiety and, in fact, after more practice, like and enjoy maths.
:-)
Labels:
Learning maths
Math Challenge 9
Think of a number (Keep the number to yourself).
Add five to it.
Multiply the total by two.
Subtract the original number twice.
Is the answer "TEN"?
Thinker: How is it done?
.
Add five to it.
Multiply the total by two.
Subtract the original number twice.
Is the answer "TEN"?
Thinker: How is it done?
.
Labels:
Maths Thinker
Math Challenge 8
Think of a number.
(Do not tell anyone).
Multiply the number by three.
Add six to it.
Divide the total by three.
Subtract the result by the original number that you kept secret.
Is the final answer "TWO"?
Thinker: How is it done? ==> Use Algebra
.
(Do not tell anyone).
Multiply the number by three.
Add six to it.
Divide the total by three.
Subtract the result by the original number that you kept secret.
Is the final answer "TWO"?
Thinker: How is it done? ==> Use Algebra
.
Labels:
Maths Thinker
How To Draw Best Fitting Straight Line
In graph analysis, we are normally given a set of co-ordinates to plot and extract the important parameters from the straight line drawn.
The data given are mostly random values that may not be lying on a straight line.
Therefore the technique of drawing this straight line on the graph becomes a crucial skill as it may results in producing inaccurate answers or outcomes.
An example is presented here for discussion.
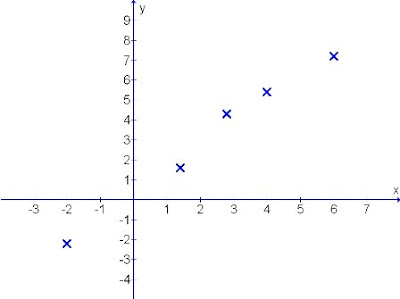
Diagram 1: Various random co-ordinates scattered over the sheet
How do we plot a suitable straight line from these few scattered co-ordinates?
Many "funny" ways exist that reflects poor understanding of the purpose for straight line plotting.
Way one:
Connecting up the points in sequence ==> Results in non-straight line end-to-end.
Way two:
Connecting the extreme two co-ordinates ==> Results in unbalanced straight line (diagram 2)
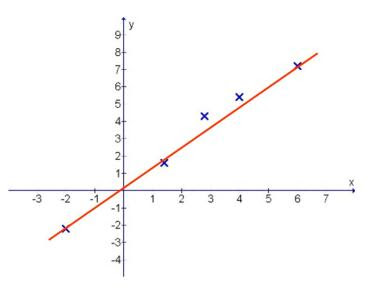
Diagram 2: Uneven gaps between points and line drawn
Here you can clearly see that there are 2 points that are above the straight line by a certain gap. The spread of the random points are not evenly balanced about the straight line drawn.
Let's see a better way to fit the line to these randomly scattered points. (Diagram 3)
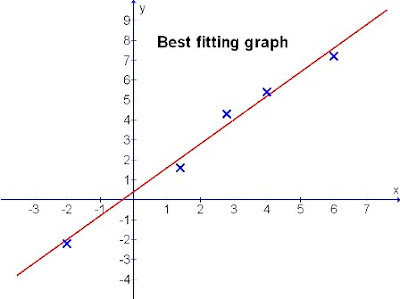
Diagram 3
In diagram 3, you can see that the scattered points are evenly balanced across the length of the straight line drawn. The gaps of the crosses are almost the same through.
This is termed the "Best fitting straight line".
Therefore in plotting a straight line, it is the evenness that counts. The spread of the points has to be balanced so that the individual errors of the given data to the line can be minimised. The line drawn is then one that will produce a more accurate results.
Never imagine that so much thoughts are needed just to plot a straight line graph, right?
:-)
The data given are mostly random values that may not be lying on a straight line.
Therefore the technique of drawing this straight line on the graph becomes a crucial skill as it may results in producing inaccurate answers or outcomes.
An example is presented here for discussion.

Diagram 1: Various random co-ordinates scattered over the sheet
How do we plot a suitable straight line from these few scattered co-ordinates?
Many "funny" ways exist that reflects poor understanding of the purpose for straight line plotting.
Way one:
Connecting up the points in sequence ==> Results in non-straight line end-to-end.
Way two:
Connecting the extreme two co-ordinates ==> Results in unbalanced straight line (diagram 2)

Diagram 2: Uneven gaps between points and line drawn
Here you can clearly see that there are 2 points that are above the straight line by a certain gap. The spread of the random points are not evenly balanced about the straight line drawn.
Let's see a better way to fit the line to these randomly scattered points. (Diagram 3)

Diagram 3
In diagram 3, you can see that the scattered points are evenly balanced across the length of the straight line drawn. The gaps of the crosses are almost the same through.
This is termed the "Best fitting straight line".
Therefore in plotting a straight line, it is the evenness that counts. The spread of the points has to be balanced so that the individual errors of the given data to the line can be minimised. The line drawn is then one that will produce a more accurate results.
Never imagine that so much thoughts are needed just to plot a straight line graph, right?
:-)
Labels:
graph
How To Get Gradient and Intercept from Two Points
Gradient and intercept are two key items to a straight line expression.
In maths, to obtain the equation of a line from two given co-ordinates, we inevitably think of graph plotting. This is one good way to obtain the answer by finding the gradient and intercept.
Let's take an example.
2 points: (1, 5) and (3, 11) are given. What is the straight line expression?
By plotting these two points on a graph, we can easily determine the gradient and intercept, and then the mathematical expression for the equation.
Diag: Graph with 2 points.
From the graph, to determine the gradient, we can check:
Gradient = change in vertical / change in horizontal = 6 / 2 = 3
The next item is the intercept, and directly from the graph, it showed the value to be 2.
Therefore, the straight line expression comes to y = 3 x + 2.
This graphical method is OK, simple and easy to do.
But is this the only way to get the straight line expression from 2 points given?
No, there is at least one other method. Don't forget maths is exciting and amazing, if one wishes it to be.
What is the other way? The answer is the use of simultaneous equations!
How so?
Note, given 2 co-ordinates and having to find 2 unknowns satisfies the basic requirement to set up 2 equations for simultaneous solving.
We know the general straight line equation to be y = mx + c.
Therefore with the known co-ordinates,
11 = m(3) + c -----(A)
5 = m(1) + c -----(B)
By elimination method, (A) - (B), gives,
6 = m(2) ===> this gives m = 6 / 2 = 3 (The gradient!)
With m = 3 found, let's put back into equation (B),
5 = (3)(1) + c ===> c = 5 - 3 = 2 (The intercept!)
Thus, the straight line equation is y = 3 x + 2. This is the same as the one obtained with graphical method.
Therefore, from the simultaneous way, we can still obtain the expression from the 2 given co-ordinates, without plotting the graph.
Either which way is fine.
What is interesting is that once you master the principles of maths, you can be flexible to choose the method that you like and still arrive at an appropriate answer.
Enjoy maths! :)
.
In maths, to obtain the equation of a line from two given co-ordinates, we inevitably think of graph plotting. This is one good way to obtain the answer by finding the gradient and intercept.
Let's take an example.
2 points: (1, 5) and (3, 11) are given. What is the straight line expression?
By plotting these two points on a graph, we can easily determine the gradient and intercept, and then the mathematical expression for the equation.

Diag: Graph with 2 points.
From the graph, to determine the gradient, we can check:
- increase of the vertical unit with reference from the 2 points as 11 - 5 = 6 units, and
- increase of the horizontal unit from the 2 points as 3 - 1 = 2 units,
Gradient = change in vertical / change in horizontal = 6 / 2 = 3
The next item is the intercept, and directly from the graph, it showed the value to be 2.
Therefore, the straight line expression comes to y = 3 x + 2.
This graphical method is OK, simple and easy to do.
But is this the only way to get the straight line expression from 2 points given?
No, there is at least one other method. Don't forget maths is exciting and amazing, if one wishes it to be.
What is the other way? The answer is the use of simultaneous equations!
How so?
Note, given 2 co-ordinates and having to find 2 unknowns satisfies the basic requirement to set up 2 equations for simultaneous solving.
We know the general straight line equation to be y = mx + c.
Therefore with the known co-ordinates,
11 = m(3) + c -----(A)
5 = m(1) + c -----(B)
By elimination method, (A) - (B), gives,
6 = m(2) ===> this gives m = 6 / 2 = 3 (The gradient!)
With m = 3 found, let's put back into equation (B),
5 = (3)(1) + c ===> c = 5 - 3 = 2 (The intercept!)
Thus, the straight line equation is y = 3 x + 2. This is the same as the one obtained with graphical method.
Therefore, from the simultaneous way, we can still obtain the expression from the 2 given co-ordinates, without plotting the graph.
Either which way is fine.
What is interesting is that once you master the principles of maths, you can be flexible to choose the method that you like and still arrive at an appropriate answer.
Enjoy maths! :)
.
Monday, 18 August 2008
How To Reduce Stress In Learning Maths
Have you been caught having to memorise maths formulae, the mathematical concepts, the "little" tricks, and the progressive steps in a given duration that many claimed to be too short?
"How to remember?"
"Why teach so fast?"
"Any simpler method?"
These are sampled questions that express the stress and anxiety that many students faced.
Though some of the components of teaching and learning can be simplified, they take time to implement with due consideration for many other factors like curriculum, key learning objectives, and quality.
What then can we do to lessen the stress that keep on coming?
The answer is to stay focus and be aware of the key objectives of the topic.
If the maths topic is about logarithm and its various laws, the objectives should be to apply the logarithmic laws to solve any related maths questions.
Do not ask questions like :-
"Why must I write the base with a smaller font size?" and
"Why do I need to add the individual logs to form a logarithmic product?".
Asking questions is definitely good for learning, but in these instances, the focus is not to dig out the history part of logarithmic studies.
The main aim is understanding the application of the laws in order to apply and solve problems. It is simply just that!
Trying to find out more than what the maths syllabus calls for within the short time frame is tantamount to facing learning disaster.
Just know that analysing too much into a subject or topic is equivalent to paralysing the learning mind. Stress, thus, appears and starts getting on your nerves!
Remove the unnecessary questions that blocks the main objectives and move along with the requirements. Pick up the extras only if you have the time and in a comfortable and relaxed mood.
Why cause undue stress and anxiety upon yourself if the key matters in maths learning is not treated properly?
Contain the scope and stay focus!
Do not dwell on things that are not the main issue and causing mental blockage. Accept what is taught for the moment, and coming back for in-depth understanding after mastering the necesary.
(NOTE: You still have to fully understand the topic, the approach explained here is to "buy" time to release some stress.)
This way, learning maths will not be that stressful and will become fun, since the basics can be managed comfortably with understanding.
:-)
"How to remember?"
"Why teach so fast?"
"Any simpler method?"
These are sampled questions that express the stress and anxiety that many students faced.
Though some of the components of teaching and learning can be simplified, they take time to implement with due consideration for many other factors like curriculum, key learning objectives, and quality.
What then can we do to lessen the stress that keep on coming?
The answer is to stay focus and be aware of the key objectives of the topic.
If the maths topic is about logarithm and its various laws, the objectives should be to apply the logarithmic laws to solve any related maths questions.
Do not ask questions like :-
"Why must I write the base with a smaller font size?" and
"Why do I need to add the individual logs to form a logarithmic product?".
Asking questions is definitely good for learning, but in these instances, the focus is not to dig out the history part of logarithmic studies.
The main aim is understanding the application of the laws in order to apply and solve problems. It is simply just that!
Trying to find out more than what the maths syllabus calls for within the short time frame is tantamount to facing learning disaster.
Just know that analysing too much into a subject or topic is equivalent to paralysing the learning mind. Stress, thus, appears and starts getting on your nerves!
Remove the unnecessary questions that blocks the main objectives and move along with the requirements. Pick up the extras only if you have the time and in a comfortable and relaxed mood.
Why cause undue stress and anxiety upon yourself if the key matters in maths learning is not treated properly?
Contain the scope and stay focus!
Do not dwell on things that are not the main issue and causing mental blockage. Accept what is taught for the moment, and coming back for in-depth understanding after mastering the necesary.
(NOTE: You still have to fully understand the topic, the approach explained here is to "buy" time to release some stress.)
This way, learning maths will not be that stressful and will become fun, since the basics can be managed comfortably with understanding.
:-)
Labels:
Learning maths,
maths anxiety
Ways To Improve Logical Learning Part Of Maths
In learning of maths, as with learning of other subjects, we need to understand our learning styles. The styles are namely, visual, auditory and kinesthetic.
Each of us has one particular dominant style. Knowing which one will thus serve us good. However, the learning style itself is still not enough, we need to also know the types of intelligence we possess.
The learning styles are used to gather information and ideas, through the senses, for the brain. But how do we process the information captured afterwards depends much on the intelligences that we also have.
In maths learning, what we need is the logical / mathematical intelligence.
This lets us do all sort of computations and comparisons that maths requires.
An example is the conversion of an expression in logarithmic form to its index form (and vice versa).
logaY = X <==> aX = Y
Though, this conversion seems simple enough, it is found that many students still have difficulties in converting the above. Do they lack this logical intelligence?
The answer is "maybe" and "maybe not".
They may have possess this logical intelligence, but has not yet enhanced it.
One way to offset this weakness in the logical comparison part of intelligence is to introduce the visual intelligence into maths learning.
What is this visual intelligence?
This is the "appearance" aspect of information processing. Here, colour, shapes, and the likes are linked up to the information.
Why introduce the visual intelligence?
The main reason is to bridge up the right and left brain, a theory that is now well-known and practiced throughout the learning and teaching communities.
Now, let's see how we can solve the logarithmic and index conversion through the use of the visual intelligence.

The examples above showed two very interesting ways to enhance the learning. :)
The first one is to replace and "beautify" the symbols with pictures or graphics to arouse retention ability.
The second one is to make use of colours to strengthen the symbols and their placements.
By seeing pictures and colours, although they are no way close to any maths topics, the learning of maths is greatly improved especially for the logical comparison portion.
Therefore, if possible, introduce as many "visuals" into maths as you can. They will make maths learning a totally new experience. Take care of intelligences and intelligences will take care of you.
Inspired ?
:=)
Each of us has one particular dominant style. Knowing which one will thus serve us good. However, the learning style itself is still not enough, we need to also know the types of intelligence we possess.
The learning styles are used to gather information and ideas, through the senses, for the brain. But how do we process the information captured afterwards depends much on the intelligences that we also have.
In maths learning, what we need is the logical / mathematical intelligence.
This lets us do all sort of computations and comparisons that maths requires.
An example is the conversion of an expression in logarithmic form to its index form (and vice versa).
logaY = X <==> aX = Y
Though, this conversion seems simple enough, it is found that many students still have difficulties in converting the above. Do they lack this logical intelligence?
The answer is "maybe" and "maybe not".
They may have possess this logical intelligence, but has not yet enhanced it.
One way to offset this weakness in the logical comparison part of intelligence is to introduce the visual intelligence into maths learning.
What is this visual intelligence?
This is the "appearance" aspect of information processing. Here, colour, shapes, and the likes are linked up to the information.
Why introduce the visual intelligence?
The main reason is to bridge up the right and left brain, a theory that is now well-known and practiced throughout the learning and teaching communities.
Now, let's see how we can solve the logarithmic and index conversion through the use of the visual intelligence.

The examples above showed two very interesting ways to enhance the learning. :)
The first one is to replace and "beautify" the symbols with pictures or graphics to arouse retention ability.
The second one is to make use of colours to strengthen the symbols and their placements.
By seeing pictures and colours, although they are no way close to any maths topics, the learning of maths is greatly improved especially for the logical comparison portion.
Therefore, if possible, introduce as many "visuals" into maths as you can. They will make maths learning a totally new experience. Take care of intelligences and intelligences will take care of you.
Inspired ?
:=)
Labels:
indices,
Learning maths,
Logarithm,
teaching maths
Benefits Of Knowing How To Solve Quadratic Equations
In elementary school, we are exposed to quadratic equations and their solving. We focus a lot on this topics which is deemed the basic of any algebraic studies.
The generic quadratic equation is y = a x2 + bx + c.
We know there are various methods to handle the quadratic equations.
There are:
Mastering all these techniques allow anyone studying maths to have the flexibility of choosing a better or suitable method that fits the nature of the question.
However, do note that if there is problem learning all these techniques at one go, click here to get some pointers.
What is the benefit?
Many maths questions are actually quadratic in expression. They may not appear so, but, on closer look, they are.
Examples:
Being able to handle the generic quadratic equation solving means having the potential to solve numerous other types of quadratic equations as listed above.
What is the obstacle if you still cannot map the quadratic solving method to the other types of expressions?
Tips:
And that's all.
Simple isn't it?
Thus, mastering any one method of handling quadratic equation allows anyone to solve many other types of quadratic equations. Therefore, it is worth the time and effort to know solving these type of mathematical expression.
Bonus information:
Let's look into this example
5x-2 - 3x-1 - 2 = 0
The first term can be modified to 5(x-1)2.
The second term can be modified to 3(x-1).
The last term will be obviously the pure number "2".
Selecting the use of quadratic formula, we can say that a = 5, b= -3 and c = -2.
Next, just apply the quadratic formula and you are close to the two answers (roots) of the equation,
x-1 = -4/10 or 1. Clear?
If not, read again... Our brain needs some mental exercise at times.
.
The generic quadratic equation is y = a x2 + bx + c.
We know there are various methods to handle the quadratic equations.
There are:
- Factoring
- Completing the Square
- Quadratic Formula
- Graphical
Mastering all these techniques allow anyone studying maths to have the flexibility of choosing a better or suitable method that fits the nature of the question.
However, do note that if there is problem learning all these techniques at one go, click here to get some pointers.
What is the benefit?
Many maths questions are actually quadratic in expression. They may not appear so, but, on closer look, they are.
Examples:
- 3 cos2 A + 2cosA + 4 = 0
- 2 (log Y)2 + 2(logY) + 3 = 0
- 4x + 3(2x) - 5 = 0
- 5x-2 - 7x-1 - 6 = 0
Being able to handle the generic quadratic equation solving means having the potential to solve numerous other types of quadratic equations as listed above.
What is the obstacle if you still cannot map the quadratic solving method to the other types of expressions?
Tips:
- Stare at the given expression
- Identify the terms that matches the x2 format.
- Identify the other two terms through the "x" format and pure number format.
- After re-writing the questions in the generic quadratic form, apply any of the method to solve this quadratic equation.
And that's all.
Simple isn't it?
Thus, mastering any one method of handling quadratic equation allows anyone to solve many other types of quadratic equations. Therefore, it is worth the time and effort to know solving these type of mathematical expression.
Bonus information:
Let's look into this example
The first term can be modified to 5(x-1)2.
The second term can be modified to 3(x-1).
The last term will be obviously the pure number "2".
Selecting the use of quadratic formula, we can say that a = 5, b= -3 and c = -2.
Next, just apply the quadratic formula and you are close to the two answers (roots) of the equation,
x-1 = -4/10 or 1. Clear?
If not, read again... Our brain needs some mental exercise at times.
.
Labels:
Learning maths
Indices & Logarithm - Less Mistakes with Proper Writing
Every symbols in mathematics serve certain purpose. The size of the symbols and numbers also represent unique meaning.
Many mistakes and confusions were made due to improper writing of the above two items that are very much key to mathematics.
Two of the topics that are commonly populated with writing errors are Indices and Logarithm.
Indices: ax = Y
Logarithm: lognA = K
From the above two examples, it is apparent that writing is crucial to give correct meaning to mathematics.
Writing therefore is an important skill while doing these two maths topics.
Discipline is needed here to maintain consistency.
What do I mean?
Let me give an example.
log2 xy = log2x + log2y
The above is a correct expression written with proper size and positioning.
If writing discipline is not maintained, it may end up as:
log2 xy = log2x + log2y (size and position error)
Do you notice the change in meaning when size changes?
The subscript "2" representing "base 2" is conveyed as "2 times y"!
This is the result of a simple "slip" of the hand in writing the size of the "2".
Can this mistake be allowed?
I guess NO!
Why run the risk of marks being deducted or effort wasted in getting wrong answers?
Write properly is the only answer to less mistakes, if not at all.
If ax = Y is written as ax = Y, how do we expect to get correct answers?
Here, you realise that maths learning is not just about mathematical concepts, human discipline and strength of concentration matters also.
Being able to write clearly and presentable is a noble capability that we should be proud to demonstrate to anyone. Strive to be focused and discipline when dealing with maths.
Happy writing! :P
.
Many mistakes and confusions were made due to improper writing of the above two items that are very much key to mathematics.
Two of the topics that are commonly populated with writing errors are Indices and Logarithm.
Indices: ax = Y
Logarithm: lognA = K
From the above two examples, it is apparent that writing is crucial to give correct meaning to mathematics.
Writing therefore is an important skill while doing these two maths topics.
Discipline is needed here to maintain consistency.
What do I mean?
Let me give an example.
log2 xy = log2x + log2y
The above is a correct expression written with proper size and positioning.
If writing discipline is not maintained, it may end up as:
log2 xy = log2x + log2y (size and position error)
Do you notice the change in meaning when size changes?
The subscript "2" representing "base 2" is conveyed as "2 times y"!
This is the result of a simple "slip" of the hand in writing the size of the "2".
Can this mistake be allowed?
I guess NO!
Why run the risk of marks being deducted or effort wasted in getting wrong answers?
Write properly is the only answer to less mistakes, if not at all.
If ax = Y is written as ax = Y, how do we expect to get correct answers?
Here, you realise that maths learning is not just about mathematical concepts, human discipline and strength of concentration matters also.
Being able to write clearly and presentable is a noble capability that we should be proud to demonstrate to anyone. Strive to be focused and discipline when dealing with maths.
Happy writing! :P
.
Know Your Limits While Learning Maths
While learning mathematics, we are always exposed to a few methods of solving a particular maths questions. The methods are taught in order to give us flexibility to select an appropriate technique to "attack" any maths problems.
Is it good then to master all the techniques taught?
The answer is to know your limits.
If you are stressed up learning so many methods, let go of the ones that you find uncomfortable with. Master the one that seems to be the best and easiest to you.
Stay on with this chosen technique of solving problems, and apply it to similar maths questions. This is the first step in the principles of correct mathematics learning.
However, do not be complacent and stay stuck! Having more methods to solve a certain maths problems is always a better and sensible course of action any maths learners should aim for.
After mastering the first selected method, move on and try using another technique that was taught. Practice till it becomes comfortable and an easy tool to use.
In mathematics, flexibility is the norm. Questions are always varied, and thus, solution has to follow suit. It is this nature of solving mathematics that makes a good maths learners achieve much in his later life.
Knowing one's limit is thus important especially when dealing with mathematics. Focus on one method first as too many at a go will only mess up the curious and greedy mind.
Understand that maths problem can be solved through the use of any one method. Even if the steps are more, it is still a way to obtain the answer. Slowly after mastering the selected method, you can explore another method that can shorten the solving process.
At least you are now more relax as you can fall back to the first method if the new technique cannot be comprehended finally.
However, having said that, do review the maths syllabus. Some syllabus do spell out that the students have to master a few methods to solve a certain type of maths questions. For that matter, you are left with no choice but to deal with them accordingly. Seek for help if necessary, and do not simply give up!
Finally a message that I like to share. "Although practice makes perfect, good practice is the one that makes perfect ultimately!"
Choose the correct principles of learning and you will not go wrong. Know your mental limits.
;)
Is it good then to master all the techniques taught?
The answer is to know your limits.
If you are stressed up learning so many methods, let go of the ones that you find uncomfortable with. Master the one that seems to be the best and easiest to you.
Stay on with this chosen technique of solving problems, and apply it to similar maths questions. This is the first step in the principles of correct mathematics learning.
However, do not be complacent and stay stuck! Having more methods to solve a certain maths problems is always a better and sensible course of action any maths learners should aim for.
After mastering the first selected method, move on and try using another technique that was taught. Practice till it becomes comfortable and an easy tool to use.
In mathematics, flexibility is the norm. Questions are always varied, and thus, solution has to follow suit. It is this nature of solving mathematics that makes a good maths learners achieve much in his later life.
Knowing one's limit is thus important especially when dealing with mathematics. Focus on one method first as too many at a go will only mess up the curious and greedy mind.
Understand that maths problem can be solved through the use of any one method. Even if the steps are more, it is still a way to obtain the answer. Slowly after mastering the selected method, you can explore another method that can shorten the solving process.
At least you are now more relax as you can fall back to the first method if the new technique cannot be comprehended finally.
However, having said that, do review the maths syllabus. Some syllabus do spell out that the students have to master a few methods to solve a certain type of maths questions. For that matter, you are left with no choice but to deal with them accordingly. Seek for help if necessary, and do not simply give up!
Finally a message that I like to share. "Although practice makes perfect, good practice is the one that makes perfect ultimately!"
Choose the correct principles of learning and you will not go wrong. Know your mental limits.
;)
Labels:
Learning maths
Solving Maths Develops Plan Foward Capability
As in any case of solving problems, solving maths also requires certain strategy and procedures. Performing the mathematical steps to realise the result need certain skills.
One of this skill is the ability to see the "path" to the result. This ability, however, is obtained when we are able to plan what to do and reveal the intermediate goals.
Solving maths is like a mini-warfare where the enemy is the result that has to be obtained. Every steps that we take to achieve our goals has to be planned for.
We need to think ahead in each steps of computation and be capable of using whatever tools available to clear the obstacles lying in front of us.
Solving maths, thus, is a good platform for anyone to gear themselves for a future of planning, or to have better planning capability.
The steps required to solve a maths problem develops one to be able to plan forward. The steps taken at every maths operation serves a certain purpose to simplify mathematical expressions or eliminate unknowns.
Studying and doing maths is therefore a necessary part of human development in that it allows the learners to develop their mind to solve real-life problems through proper planning.
So to developing minds, cheers to maths!
.
One of this skill is the ability to see the "path" to the result. This ability, however, is obtained when we are able to plan what to do and reveal the intermediate goals.
Solving maths is like a mini-warfare where the enemy is the result that has to be obtained. Every steps that we take to achieve our goals has to be planned for.
We need to think ahead in each steps of computation and be capable of using whatever tools available to clear the obstacles lying in front of us.
Solving maths, thus, is a good platform for anyone to gear themselves for a future of planning, or to have better planning capability.
The steps required to solve a maths problem develops one to be able to plan forward. The steps taken at every maths operation serves a certain purpose to simplify mathematical expressions or eliminate unknowns.
Studying and doing maths is therefore a necessary part of human development in that it allows the learners to develop their mind to solve real-life problems through proper planning.
So to developing minds, cheers to maths!
.
Labels:
Learning maths
Why Do We Study Quadratic Equation?
In maths class, we are hammered with expressions after expressions of quadratic equations. We are taught how to solve for its roots. We are taught all the necessary methods or mathematical techniques to handle quadratic equations.
But after all these, what is the purpose?
This is the question many students of maths studies ask.
Do we need this "quadratic" knowledge in working life?
See the diagrams and photos below. They will enlighten you.

The communication dish is parabolic in shape. Parabolic is the equivalent to quadratic mathematically. Engineers need to understand quadratic equation to design this beautiful profile.
 This wok is designed using quadratic expression. With this, food can be fried to our liking!
This wok is designed using quadratic expression. With this, food can be fried to our liking!
Without quadratic equation, who knows how a wok would look like.
.
.
Here you see that eye-glass lens are constructed with curves matching that of the quadratic equation.
Light is thus controlled to give good image to our eyes.
Quadratic equations to the rescue, right?
.
.
.
.
.
.
Other examples are:
1) Distance travelled given by the quadratic equation s = ut + (1/2) a t2
2) Electrical characteristics of a MOSFET (Transistor device)
i = k [(Vg - Vt)VD - (1/2)Vd2]
So now do you still wonder why you study quadratic equations?
Maths do have a purpose in our daily life. Rest assure that you are studying maths for a good cause.
:-)
But after all these, what is the purpose?
This is the question many students of maths studies ask.
Do we need this "quadratic" knowledge in working life?
See the diagrams and photos below. They will enlighten you.

The communication dish is parabolic in shape. Parabolic is the equivalent to quadratic mathematically. Engineers need to understand quadratic equation to design this beautiful profile.
 This wok is designed using quadratic expression. With this, food can be fried to our liking!
This wok is designed using quadratic expression. With this, food can be fried to our liking!Without quadratic equation, who knows how a wok would look like.
.
.

Here you see that eye-glass lens are constructed with curves matching that of the quadratic equation.
Light is thus controlled to give good image to our eyes.
Quadratic equations to the rescue, right?
.
.
.
.
.
.
Other examples are:
1) Distance travelled given by the quadratic equation s = ut + (1/2) a t2
2) Electrical characteristics of a MOSFET (Transistor device)
i = k [(Vg - Vt)VD - (1/2)Vd2]
So now do you still wonder why you study quadratic equations?
Maths do have a purpose in our daily life. Rest assure that you are studying maths for a good cause.
:-)
Labels:
Algebra
Merit of Grouping in Maths Solving
For those who do maths at above elementary level, you will encounter many terms involved in the already many steps to solve a mathematical question.
Example is the solution of Partial fraction, that is highly needed in calculus.
One of the steps needed is the comparing of coefficients to extract out equations to determine the numerators in the individual terms of the partial fractions.
An example is shown below.
x - 3 = A x2 + B x (x + 1) + C (x - 2)
How do we solve for the unknown A, B and C?
One useful technique is to do "grouping" of relevant terms.
This is a simple yet powerful method that make the process of solving maths less confusing as it serves to gather common or liked term in the same boundaries.
What I mean is ....
From the above example, we can rewrite them as,
x - 3 = A x2 + Bx (x + 1) + C (x - 2)
==> x - 3 = A x2 + Bx2 + Bx + Cx - 2C
==> x - 3 = (A + B)x2 +(B + C)x - 2C
Here, you can see that the coefficient of the terms can be equated nicely to be :-
x2 term: (A + B) = 0
x term: (B + C) = 1
Constant: 2C = 3
From herer A, B and C can be easily determined comfortably.
Thus, grouping has the ability to simplify the thinking steps due to clarity as reflected above.
Another example is in Indices simplification.
Take the example of 10n5n/2 / 20n/4.
We cannot see any way to combine the different base number (10, 5 and 20) unless we split them into their lowest factors. (Don't lost focus now, we are aiming for Grouping technique!)
10n = (5 x 2 )n
20n = (2 x 2 x 5)n
Rewriting to prepare for grouping,
(5 x 2 )n5n/2 / (2 x 2 x 5)n/4
==> 5(n + n/2 - n/4) 2n- n/4 - n/4
==> 55/4n 2n/2
Here again, you can see the merit of grouping the common base number in order to perform the Indices operation.
Maths is "tricky" at times, but isn't this to train our mind to stay active and flexible to counter any challenges put forward. It actually enhances our self-esteem and confidence to handle problems in real life.
Happy grouping .....
:-)
Example is the solution of Partial fraction, that is highly needed in calculus.
One of the steps needed is the comparing of coefficients to extract out equations to determine the numerators in the individual terms of the partial fractions.
An example is shown below.
x - 3 = A x2 + B x (x + 1) + C (x - 2)
How do we solve for the unknown A, B and C?
One useful technique is to do "grouping" of relevant terms.
This is a simple yet powerful method that make the process of solving maths less confusing as it serves to gather common or liked term in the same boundaries.
What I mean is ....
From the above example, we can rewrite them as,
x - 3 = A x2 + Bx (x + 1) + C (x - 2)
==> x - 3 = A x2 + Bx2 + Bx + Cx - 2C
==> x - 3 = (A + B)x2 +(B + C)x - 2C
Here, you can see that the coefficient of the terms can be equated nicely to be :-
x2 term: (A + B) = 0
x term: (B + C) = 1
Constant: 2C = 3
From herer A, B and C can be easily determined comfortably.
Thus, grouping has the ability to simplify the thinking steps due to clarity as reflected above.
Another example is in Indices simplification.
Take the example of 10n5n/2 / 20n/4.
We cannot see any way to combine the different base number (10, 5 and 20) unless we split them into their lowest factors. (Don't lost focus now, we are aiming for Grouping technique!)
10n = (5 x 2 )n
20n = (2 x 2 x 5)n
Rewriting to prepare for grouping,
(5 x 2 )n5n/2 / (2 x 2 x 5)n/4
==> 5(n + n/2 - n/4) 2n- n/4 - n/4
==> 55/4n 2n/2
Here again, you can see the merit of grouping the common base number in order to perform the Indices operation.
Maths is "tricky" at times, but isn't this to train our mind to stay active and flexible to counter any challenges put forward. It actually enhances our self-esteem and confidence to handle problems in real life.
Happy grouping .....
:-)
Indices | Big and Small concept
In the study of indices, symbols are written with two sizes and in two different positions. They have their own unique meanings.
a2 means a times a, or simply a x a.
(a + b)2 means (a + b) x (a + b).
(anything)3 means (anything) x (anything) x (anything).
Therefore, from above examples, we can see that "anything" operated by a small number higher up above it means repetition by that number of times (defined by that little number).
Mistakes normally made:
(a + b)2 ==> a2 + b2 This is wrong!
a2 - b2 ==> (a - b) 2 This is also incorrect!
Reason
The "2" is a power and not a factor. It means repetition. And therefore cannot be factorised.
The "2" is written above the normal line (called the base), and thus has "bigger" power than the base element.
The correct answer to the mistakes:
(a + b)2 = ( a + b) ( a + b) = a2 + 2ab + b2
a2 - b2 = ( a x a ) - ( b x b ) = (a - b ) ( a + b ).
To summarise, the "smaller" number (or letter) makes the "larger" base repeats the number of times indicated by that small number.
Principles of mathematics and its indices' concept .....
Understand the principles and concepts, and you will be fine.
For more common mistakes in indices, click here.
.
a2 means a times a, or simply a x a.
(a + b)2 means (a + b) x (a + b).
(anything)3 means (anything) x (anything) x (anything).
Therefore, from above examples, we can see that "anything" operated by a small number higher up above it means repetition by that number of times (defined by that little number).
Mistakes normally made:
(a + b)2 ==> a2 + b2 This is wrong!
a2 - b2 ==> (a - b) 2 This is also incorrect!
Reason
The "2" is a power and not a factor. It means repetition. And therefore cannot be factorised.
The "2" is written above the normal line (called the base), and thus has "bigger" power than the base element.
The correct answer to the mistakes:
(a + b)2 = ( a + b) ( a + b) = a2 + 2ab + b2
a2 - b2 = ( a x a ) - ( b x b ) = (a - b ) ( a + b ).
To summarise, the "smaller" number (or letter) makes the "larger" base repeats the number of times indicated by that small number.
Principles of mathematics and its indices' concept .....
Understand the principles and concepts, and you will be fine.
For more common mistakes in indices, click here.
.
Labels:
indices
Tips To Reduce Errors Doing Simultaneous Equations
Solving simultaneous equations involves many simple steps. The simple steps mostly include addition, subtraction and multiplication.
Though the mathematical operations are simple, mistakes made while solving simultaneous equations are aplenty. The errors are mostly "slip-of-the-mind" human errors.
To review the elimination method employed to solve simultaneous equations, please click here.
How then are we to reduce these careless errors?
Here, I propose 2 tips.
Tip one
Make use of addition instead of subtraction to eliminate the selected unknown.
Example: ( to eliminate unknown "y")
7x + 2y = 11 --- (A)
-5x + 2y = -1 --- (B)
In normal doing, we perform (A) - (B) equation subtraction. But what is the risk?
The result may end up as 2x + 0 = 10 !
The correct answer should be 12x + 0 = 12.
Why the error?
This is because our brain is use to addition more than subtraction. Therefore the "slip-of- the-mind" error happened.
Mentally doing 7x - (-5x) is harder to operate with.
Refer to this post to understand why our brain likes addition.
So how?
Negate the equation (B) so that we can perform addition.
(-5x + 2y) times (-1) = -1 times (-1)
will become 5x - 2y = 1 ----(C)
Rewriting the question,
7x + 2y = 11 ----(A)
5x - 2y = 1 ----(C)
This becomes simpler!
We now need to ADD the 2 equations. (Instead of the risky subtraction).
(A) + (C) : 12x + 0 = 12 <== This is the correct result that we want, risk-free!
Message: Negate the unknown variable of one equation and do ADDITION to remove it.
Tip two
Avoid making the number (coefficient) bigger through multiplication.
Example:
9x + 2y = 13 --- ( K )
x - 4y = -7 --- ( L )
Here, we have the option to remove either the "x" or the "y".
Which to select depends on the proper selection of multiplication factor in order not to make the coefficient big.
Case 1: Remove "x".
We need to multiply equation (L) by 9 to cause the first term (x) to be the same as that in equation (k), so as to eliminate the "x" unknown.
What happened?
Equation (L) became 9x - 36 y = - 63 !
Look at the coefficient of "y" ===> It became a GIANT!
Case 2: Remove unknown "y".
Multiply equation (k) by 2. This produces equation (k) as 18x + 4 y = 26.
This is still manageable. And less error will occur since big number is harder to handle.
Message: Seek to multiply coefficient such that the resultant equation has smaller number.
I have seen many maths students fumbling with these simple operations, and making many unnecessary mistakes.
I do hope that these two little tips will aid you and any maths learners of simultaneous equations to reduce errors.
:-P
Though the mathematical operations are simple, mistakes made while solving simultaneous equations are aplenty. The errors are mostly "slip-of-the-mind" human errors.
To review the elimination method employed to solve simultaneous equations, please click here.
How then are we to reduce these careless errors?
Here, I propose 2 tips.
Tip one
Make use of addition instead of subtraction to eliminate the selected unknown.
Example: ( to eliminate unknown "y")
7x + 2y = 11 --- (A)
-5x + 2y = -1 --- (B)
In normal doing, we perform (A) - (B) equation subtraction. But what is the risk?
The result may end up as 2x + 0 = 10 !
The correct answer should be 12x + 0 = 12.
Why the error?
This is because our brain is use to addition more than subtraction. Therefore the "slip-of- the-mind" error happened.
Mentally doing 7x - (-5x) is harder to operate with.
Refer to this post to understand why our brain likes addition.
So how?
Negate the equation (B) so that we can perform addition.
(-5x + 2y) times (-1) = -1 times (-1)
will become 5x - 2y = 1 ----(C)
Rewriting the question,
7x + 2y = 11 ----(A)
5x - 2y = 1 ----(C)
This becomes simpler!
We now need to ADD the 2 equations. (Instead of the risky subtraction).
(A) + (C) : 12x + 0 = 12 <== This is the correct result that we want, risk-free!
Message: Negate the unknown variable of one equation and do ADDITION to remove it.
Tip two
Avoid making the number (coefficient) bigger through multiplication.
Example:
9x + 2y = 13 --- ( K )
x - 4y = -7 --- ( L )
Here, we have the option to remove either the "x" or the "y".
Which to select depends on the proper selection of multiplication factor in order not to make the coefficient big.
Case 1: Remove "x".
We need to multiply equation (L) by 9 to cause the first term (x) to be the same as that in equation (k), so as to eliminate the "x" unknown.
What happened?
Equation (L) became 9x - 36 y = - 63 !
Look at the coefficient of "y" ===> It became a GIANT!
Case 2: Remove unknown "y".
Multiply equation (k) by 2. This produces equation (k) as 18x + 4 y = 26.
This is still manageable. And less error will occur since big number is harder to handle.
Message: Seek to multiply coefficient such that the resultant equation has smaller number.
I have seen many maths students fumbling with these simple operations, and making many unnecessary mistakes.
I do hope that these two little tips will aid you and any maths learners of simultaneous equations to reduce errors.
:-P
Labels:
Algebra
Subscribe to:
Posts (Atom)

+copy.jpg)






