How To Get Gradient and Intercept from Two Points

Gradient and intercept are two key items to a straight line expression.

In maths, to obtain the equation of a line from two given co-ordinates, we inevitably think of graph plotting. This is one good way to obtain the answer by finding the gradient and intercept.

Let's take an example.

2 points: (1, 5) and (3, 11) are given. What is the straight line expression?

By plotting these two points on a graph, we can easily determine the gradient and intercept, and then the mathematical expression for the equation.




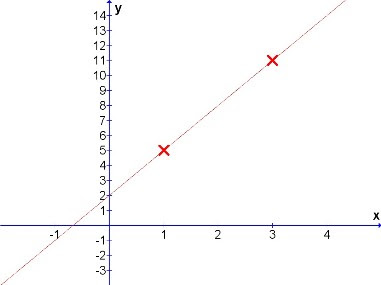
Diag: Graph with 2 points.

From the graph, to determine the gradient, we can check:

• increase of the vertical unit with reference from the 2 points as 11 - 5 = 6 units, and


• increase of the horizontal unit from the 2 points as 3 - 1 = 2 units,

Gradient = change in vertical / change in horizontal = 6 / 2 = 3

The next item is the intercept, and directly from the graph, it showed the value to be 2.

Therefore, the straight line expression comes to y = 3 x + 2.

This graphical method is OK, simple and easy to do.

But is this the only way to get the straight line expression from 2 points given?

No, there is at least one other method. Don't forget maths is exciting and amazing, if one wishes it to be.

What is the other way? The answer is the use of simultaneous equations!

How so?

Note, given 2 co-ordinates and having to find 2 unknowns satisfies the basic requirement to set up 2 equations for simultaneous solving.

We know the general straight line equation to be y = mx + c.

Therefore with the known co-ordinates,

11 = m(3) + c -----(A)

5 = m(1) + c -----(B)

By elimination method, (A) - (B), gives,

6 = m(2) ===> this gives m = 6 / 2 = 3 (The gradient!)

With m = 3 found, let's put back into equation (B),

5 = (3)(1) + c ===> c = 5 - 3 = 2 (The intercept!)

Thus, the straight line equation is y = 3 x + 2. This is the same as the one obtained with graphical method.

Therefore, from the simultaneous way, we can still obtain the expression from the 2 given co-ordinates, without plotting the graph.

Either which way is fine.

What is interesting is that once you master the principles of maths, you can be flexible to choose the method that you like and still arrive at an appropriate answer.

Enjoy maths! :)

.