However, have you wondered what is the relationship between them?
If we want to maintain the volume of an box but reduce its surface area, is it possible?
Or does the volume ALWAYS increases with increase in its surface area?
How about reduction in surface area? Will the volume also reduce?
Let us throw some numbers into an example to figure out the answers.
For simplicity, let us use a simple box. (Diagram 1)

<== Diagram 1 Box of diagram 1 has a : Volume = (2 x 8 ) x 4 = 64 cubic units
Surface area = 2 (2 x 8 ) + 2(4 x 2) + 2(8 x 4) = 112 square units
.
.
Let modify the box (Diagram 2) to another dimension and see its geometric parameters.

<== Diagram 2 Volume = ( 4 x 4 ) x 4 = 64 cubic units
Surface area = (4 x 4) x 6 sides = 96 square units
Note, the volume remained but....
the surface area has reduced!
This saves material, right?
How about another dimension (Diagram 3)?
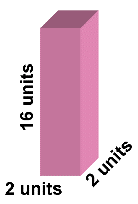
<== Diagram 3 ( A tall box!) Volume = (2 x 2 ) x 16 = 64 cubic units
Surface area = 2(2x2) + 4(2x 16) = 136 square units
What now?
The volume again remained,
but the surface area has increased!
.
What is the conclusion from here?
It is observed that althought the volume of the box has not changed, their surface areas has changed. The direction of change( increase or decrease), however, is on a case by case basis.
This concluded that there is no relationship between volume and surface area of any object.
Therefore don't be tricked into reckoning that surface area increase will cause a definite increase in volume. Likewise for reduction also.
Hope you gain much from here.
Geometry is exciting and mysterious at the same time, right?
For relationship comparsion between another set of geometrical parameters, perimeter and area, click here.
.
+copy.jpg)







2 comments:
But what if that volume was held in jelly suspended in a doughnut and straws were inserted into the doughnut while simultaneously applying a constant downward force? I remain skeptical
Forget about jelly donuts and straws. That Homer Simpson type of thinking is inherently flawed. Think of it this way: a wine bottle holds 750 ml of liquid. But if you made it as thin as a spaghetti noodle it would have to stretch across the street to still hold the same amount.
Post a Comment