Who Says The Compass Triangle Is Right-Angled?

A simple way to obtain a right-angled triangle is to draw a triangle with its corners touching the edge of a circle with its diameter as one side of the triangle.

Look at this post for details on what I am talking (or rather writing) about.

However, the question is how do we know it is truly a right-angled triangle?

The answer is "Go back to basic and prove it is!".... (or it is not)

This ability to prove will enhance your understanding of its principles.

Let the spirit of the mathematician starts flourishing ...

A diagram to simplify explanation is shown herein.

Our target: To prove that Angle C is 90 degree.



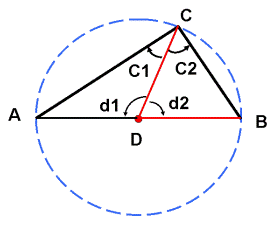
Two key items exist here. They are:

1) Length DA = DC & Length DC = DB,
since they are the radius of the circle

2) Angle C1 = Angle A & Angle C2 = Angle B,
due to the facts in item 1) above.

These 2 key points will ensure that angle C is 90 degree (or right-angle).

Moving on ...

Angle d2 = 180⁰ - Angle C2 - Angle B = 180⁰ - 2 x (Angle C2)

Angle d1 = 180⁰ - Angle d2

Which makes Angle d1 = 180⁰ - [ 180⁰ - 2 x (Angle C2) ]

This produces an important observation: Angle d1 = 2 x (Angle C2).

Also Angle A + Angle C1 + Angle d1= 180⁰, which also means,
===> [ 2 x Angle C1 ] + Angle d1= 180⁰.

Re-writing the above gives [ 2 x Angle C1 ] + 2 x (Angle C2) = 180⁰

Factorising the above equation yields:
2 x (Angle C1 + Angle C2) = 180⁰ ---(1)

Hang on, we are coming to the end ...

(Our target) Angle C = Angle C1 + Angle C2

From equation (1),
we can show that Angle C = Angle C1 + Angle C2 = 90⁰!

Therefore, it is true that
Compass Triangle has Angle C as right-angle.

Hurray!! Eureka!!

Fall back to maths basic if in doubt. The skill picked up will serve you good in the application of maths theory.

:P