The height factor of the geometrical outlook is presented in the 3-dimensional view.
But does it really present the object with a complete understanding of its shape?
There may be assumptions made if the angle of view is not appropriate.
The assumptions may be wrong!
Let me cite one example below.
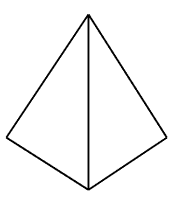
From looking at the shape presented on the left, can you tell whether the shape is that of a tetrahedron or pyramid?
Rather difficult isn't it?
It is almost impossible to tell!
Therefore, NET comes in useful in this aspect.
So, what is this net about?
Net is a different way of presenting shape. It utilises only 2-dimensional view. It is actually a 3-D object "flattened" into 2-D perspective.
The usefulness of net can be seen from the answer it presents below using the above object as reference.
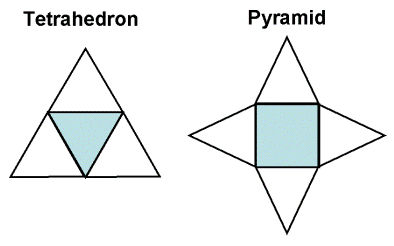
Here, if the net of the object is shown, as compared to its 3-D version, the message is clearly presented.
If the object is a tetrahedron, then the net is that of the left.
If the object is a pyramid, then the net is that of the right.
Thus, net in geometry serves its purpose in showing a clearer idea of shape when the 3-D perspective is not sufficient to reveal all details.
One common application of net is in ORIGAMI, an interesting paper folding activity liked by many.
:)
+copy.jpg)







No comments:
Post a Comment