Principle of Speed Calculation

I have noticed many questions regarding the same type of speed and time analysis.

The question asked about the time taken when two persons or cars travelling at different speed and opposite direction meet each other.

A quick way to solve this question for its time is to apply the below:

Time taken = Total distance between the two objects / Total sum of the two speeds

However, what if we forgot this so-called formula?

As Albert Einstein once said "Education is what is left after all else is forgotten".

This is very true in learning, especially for maths.

If you forgot the formula to a question and without understanding its concepts and principles, do you think you can solve that question?

Yes, only by accident, if you are lucky.

Understanding the principles is very important as it enables you to solve any question starting from basic if all else has been "returned to the teacher".

Let us look at an example.



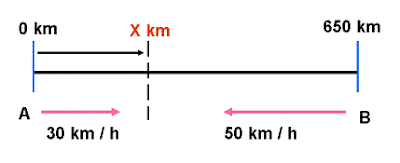
If 2 cars travelling at the speed of 30 km/h and 50 km/h meet at a distance X km away from the starting point of A, what is the time they will meet if they start off at the same time? The distance between them is 650 km apart.

Quick way to solve: T = 650 / (30 + 50) = 650 / 80 = 8.125 hrs (from start time).

From first principle:

Let the distance they meet be X km (from A point).

Since the time they meet is the same from A and B starting points,

X / 30 = (650 - X) / 50 ==> To find the value of X

(X / 30) + (X /50) = 650 /50 = 13

(50X + 30X) / 1500 = 13

80X = 1500 times 13 = 19500 ===> X = 19500 / 80 = 240.375 km

Time taken (T) for them to meet = X / 30 = 8.125 hrs (from start time).

Look here:

T = 19500/ (30 x80) hrs or

T = (19500/30) / 80 = 650 / 80 hrs

The "650" above (in bold) isn't it equal to the distance apart between the 2 cars?

The "80" above (in bold) isn't it equal to the total sum of the 2 speeds?

The working from first principle produces the SAME answer as the quick method!

But the major difference is that the solution from the Quick way has no long-lasting impact on learning as compared to the latter technique, which bank on understanding of principles of speed, time and distance.

Therefore, which way do you prefer (for longer retention of knowledge)?

:)